
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y2<y3<y1 | D. | y3<y2<y1 |
分析 先求出二次函数y=3(x-2)2+k的图象的对称轴,然后判断出A(-3,y1),B(3,y2),C(4,y3)在抛物线上的位置,再求解.
解答 解:∵二次函数y=3(x-2)2+k中a=3>0
∴抛物线开口向上,对称轴为x=-$\frac{b}{2a}$=2,
∵B(3,y2),C(4,y3)中横坐标均大于2,
∴它们在对称轴的右侧y3>y2.
A(-3,y1)中横坐标小于2,
∵它在对称轴的左侧,它关于x=2的对称点为2×2-(-3)=7,
A点的对称点是D(7,y1)
7>4>3,
∵a>0时,抛物线开口向上,在对称轴的右侧y随x的增大而增大,
∴y1>y3>y2.
故选:C.
点评 本题考查了二次函数图象上点的坐标特征,本题的关键是找到A点的对称点;掌握二次函数y=ax2+bx+c(a≠0)的图象性质.


科目:初中数学 来源: 题型:解答题
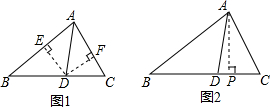 让我们来共同探究“三角形的角平分线”的特殊性质:
让我们来共同探究“三角形的角平分线”的特殊性质:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.2(1+x)2=3 | B. | 3.2(1-x)2=3 | C. | 3(1+x)2=3.2 | D. | 3(1-x)2=3.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,它正在直播排球比赛 | |
| B. | 抛掷5枚硬币,结果是2个正面朝上与3个反面朝上 | |
| C. | 黑暗中从一大串钥匙中随便选中一把,用它打开了门 | |
| D. | 投掷一枚普通的正方体骰子,正面朝上的数不是奇数便是偶数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
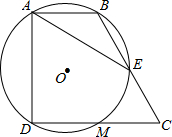 如图,已知直角梯形ABCD中,∠BAD=∠CDA=90°,CD=2AB,过A、B、D三点的⊙O分别交BC、CD于E、M.
如图,已知直角梯形ABCD中,∠BAD=∠CDA=90°,CD=2AB,过A、B、D三点的⊙O分别交BC、CD于E、M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com