
 ČēĶ¼£¬Ö±Ļßy=kx-3ÓėxÖį”¢yÖį·Ö±š½»ÓŚB”¢CĮ½µć£¬ĒŅOC=2OB
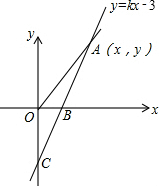
ČēĶ¼£¬Ö±Ļßy=kx-3ÓėxÖį”¢yÖį·Ö±š½»ÓŚB”¢CĮ½µć£¬ĒŅOC=2OB·ÖĪö £Ø1£©Ź×ĻČĒóµĆÖ±Ļßy=kx-3ÓėyÖįµÄ½»µć£¬ŌņOCµÄ³¤¶Č¼“æÉĒó½ā£¬½ų¶ųĒóµĆBµÄ×ų±ź£¬°ŃBµÄ×ų±ź“śČė½āĪöŹ½¼“æÉĒóµĆkµÄÖµ£»
£Ø2£©øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½¼“æÉĒó½ā£»ŌŁĄūÓĆŗÆŹż¹ŲĻµŹ½¼“æÉµĆ³ö½įĀŪ£»
£Ø3£©·ÖČżÖÖĒéæö£¬ĄūÓƵČŃüČż½ĒŠĪµÄŠŌÖŹ¼“æÉµĆ³ö½įĀŪ£®
½ā“š ½ā£ŗ£Ø1£©ŌŚy=kx-3ÖŠ£¬Įīx=0£¬Ōņy=-3£¬
”ąCµÄ×ų±źŹĒ£Ø0£¬-3£©£¬OC=3£¬
”ßOC=2OB£¬
”ąOB=$\frac{1}{2}$OC=$\frac{3}{2}$£¬
ŌņBµÄ×ų±źŹĒ£ŗ£Ø$\frac{3}{2}$£¬0£©£¬
°ŃBµÄ×ų±ź“śČėy=kx-3£¬µĆ£ŗ$\frac{3}{2}$k-3=0£¬
”ąk=2£»
£Ø2£©OB=$\frac{3}{2}$£¬
ŌņS=$\frac{1}{2}$”Į$\frac{3}{2}$£Ø2x-3£©=$\frac{3}{2}$x-$\frac{9}{4}$£»
”ß”÷AOBµÄĆ껿ĪŖ$\frac{9}{4}$£»
”ą$\frac{3}{2}$x-$\frac{9}{4}$=$\frac{9}{4}$£¬
”ąx=3£¬
ŌņAµÄ×ų±źŹĒ£Ø3£¬3£©£»
£Ø3£©ÉčP£Øm£¬0£©£¬£Øm£¾0£©
ÓÉ£Ø1£©£Ø2£©ÖŖ£¬A£Ø3£¬3£©£¬B£Ø$\frac{3}{2}$£¬0£©£¬
”ąAB2=£Ø3-$\frac{3}{2}$£©2+9=$\frac{45}{4}$£¬AP2=£Øm-3£©2+9=m2-6m+18£¬BP2=£Øm-$\frac{3}{2}$£©2£¬
”ß”÷ABPĪŖµČŃüČż½ĒŠĪ£¬
¢Łµ±AB=APŹ±£¬”ąAB2=AP2£¬
”ą$\frac{45}{4}$=m2-6m+18£¬
”ąm=-$\frac{3}{2}$£ØÉį£©»ņm=$\frac{9}{2}$£¬
”ąP£Ø$\frac{9}{2}$£¬0£©
¢Śµ±AB=BPŹ±£¬”ąAB2=BP2£¬
”ą$\frac{45}{4}$=£Øm-$\frac{3}{2}$£©2£¬
”ąm=$\frac{3-3\sqrt{5}}{2}$£ØÉį£©»ņm=$\frac{3+3\sqrt{5}}{2}$£¬
”ąP£Ø$\frac{3+3\sqrt{5}}{2}$£¬0£©
¢Ūµ±AP=BPŹ±£¬AP2=BP2£¬
”ąm2-6m+18=£Øm-$\frac{3}{2}$£©2£¬
”ąm=$\frac{21}{4}$£¬
”ąP£Ø$\frac{21}{4}$£¬0£©
Āś×ćĢõ¼žµÄPµÄ×ų±źĪŖP£Ø$\frac{9}{2}$£¬0£©»ņ£Ø$\frac{21}{4}$£¬0£©»ņ£Ø$\frac{3+3\sqrt{5}}{2}$£¬0£©£®
µćĘĄ “ĖĢāŹĒŅ»“ĪŗÆŹż×ŪŗĻĢā£¬Ö÷ŅŖæ¼²éĮĖČż½ĒŠĪµÄĆ껿£¬µČŃüČż½ĒŠĪµÄŠŌÖŹ£¬“ż¶ØĻµŹż·Ø£¬ĢåĻÖĮĖ·ÖĄąĢÖĀŪµÄĖ¼Ļė£¬½ā±¾ĢāµÄ¹Ų¼üŹĒ·ÖĄąĢÖĀŪµÄĖ¼Ļė·Ö±š½ØĮ¢·½³Ģ£¬“ĖĄąĢāÄ滹æÉŅŌ½čÖś“¹Ö±Ę½·ÖĻߥ“Č·¶ØµćPµÄ×ų±ź£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 100Ģõ | B£® | 200Ģõ | C£® | 300Ģõ | D£® | 400Ģõ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬AEŹĒ”ĻBACµÄĘ½·ÖĻߣ¬”ĻABCµÄĘ½·ÖĻßBM½»AEÓŚµćM£¬µćOŌŚABÉĻ£¬ŅŌµćOĪŖŌ²ŠÄ£¬OBµÄ³¤ĪŖ°ė¾¶µÄŌ²¾¹żµćM£¬½»BCÓŚµćG£¬½»ABÓŚµćF£®
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬AEŹĒ”ĻBACµÄĘ½·ÖĻߣ¬”ĻABCµÄĘ½·ÖĻßBM½»AEÓŚµćM£¬µćOŌŚABÉĻ£¬ŅŌµćOĪŖŌ²ŠÄ£¬OBµÄ³¤ĪŖ°ė¾¶µÄŌ²¾¹żµćM£¬½»BCÓŚµćG£¬½»ABÓŚµćF£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
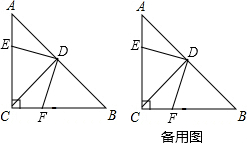 ŌŚ”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=BC£¬DŹĒABµÄÖŠµć£¬µćEŹĒ±ßACÉĻµÄŅ»¶Æµć£¬µćFŹĒ±ßBCÉĻµÄŅ»¶Æµć£®
ŌŚ”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=BC£¬DŹĒABµÄÖŠµć£¬µćEŹĒ±ßACÉĻµÄŅ»¶Æµć£¬µćFŹĒ±ßBCÉĻµÄŅ»¶Æµć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā

| A£® | 2øö | B£® | 3øö | C£® | 4øö | D£® | 5øö |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -1 | B£® | 1 | C£® | 0 | D£® | ”Ą1 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
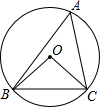 ČēĶ¼£¬”ŃOŹĒ”÷ABCµÄĶā½ÓŌ²£¬”ĻOCB=40”ć£¬Ōņ”ĻAµÄ“óŠ”ĪŖ£Ø””””£©
ČēĶ¼£¬”ŃOŹĒ”÷ABCµÄĶā½ÓŌ²£¬”ĻOCB=40”ć£¬Ōņ”ĻAµÄ“óŠ”ĪŖ£Ø””””£©| A£® | 40”ć | B£® | 50”ć | C£® | 80”ć | D£® | 100”ć |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ČēĶ¼£¬µćA”¢B”¢CŌŚ”ŃOÉĻ£¬”ĻOBC=18”ć£¬Ōņ”ĻA=£Ø””””£©
ČēĶ¼£¬µćA”¢B”¢CŌŚ”ŃOÉĻ£¬”ĻOBC=18”ć£¬Ōņ”ĻA=£Ø””””£©| A£® | 18”ć | B£® | 36”ć | C£® | 72”ć | D£® | 144”ć |
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com