
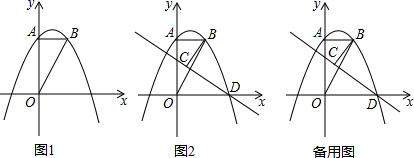
���� ��1����������õ���A��B�����꣬�����Ǵ�����κ�������ʽ���г�����ϵ��b��c�ķ����飬ͨ���ⷽ�������������ǵ�ֵ��
��2����ͼ������B��BF��x����F����������AOFB��Ȼ������ת�����������D�����ꣻ�ֱ����C��D��CE��AB��DG��OB������ֱ���E��G������������Ǻ�������õ���$\frac{CE}{DG}$=$\frac{CB}{DB}$����OB•DG=OD•BF����ֱ�ǡ�AOB�У��ɹ��ɶ������OB=BD=2$\sqrt{5}$��������������DG=$\frac{8\sqrt{5}}{5}$������CE=$\frac{8}{5}$��BE=$\sqrt{C{B}^{2}-C{E}^{2}}$������߶μ�ĺͲ��ϵ�����C�����꣮
���  �⣺��1��������õ���A��0��4����B��2��4����
�⣺��1��������õ���A��0��4����B��2��4����
����A��B���������y=-$\frac{1}{2}{x}^{2}$+bx+c��
��$\left\{\begin{array}{l}{c=4}\\{-2+2b+c=4}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=1}\\{c=4}\end{array}\right.$��
�ʸö��κ�������ʽΪ��y=-$\frac{1}{2}{x}^{2}$+x+4��
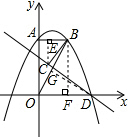
��2����ͼ������B��BF��x����F��
���ı���AOFB�Ǿ��Σ�
��OF=AB=2��BF=AO=4��
����ת�����ʿ�֪��BD=OB��BC=BA=2����DBC=��OBA��
��OD=2OF=4��
���D�������ǣ�4��0�����ֱ����C��D��CE��AB��DG��OB������ֱ���E��G��
���CEB=��BGD=90�㣬
��$\frac{CE}{DG}$=$\frac{CB}{DB}$��
��ֱ�ǡ�AOB�У�OB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$��
��BD=2$\sqrt{5}$��
��OB•DG=OD•BF��
��DG=$\frac{8\sqrt{5}}{5}$��
��$\frac{CE}{\frac{8\sqrt{5}}{5}}$=$\frac{2}{2\sqrt{5}}$����CE=$\frac{8}{5}$��BE=$\sqrt{C{B}^{2}-C{E}^{2}}$=$\sqrt{{2}^{2}-��\frac{8}{5}��^{2}}$=$\frac{6}{5}$��
���C����������2-$\frac{6}{5}$��4-$\frac{8}{5}$��������$\frac{4}{5}$��$\frac{12}{5}$����
���� ���⿼���˴���ϵ��������κ����Ľ���ʽ�����ε����ʡ����Ǻ����Ķ��壮�����ѶȽϴ�ע�����շ���˼�������ν��˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com