Question

若二次方程（b-c）x²+（c-a）x+（a-b）=0有两个相等的实数根，且b≠c，则a，b，c之间的关系式是

1. A.
   b=\frac{a-c}{2}
2. B.
   b=\frac{a+c}{2}
3. C.
   a=\frac{b+c}{2}
4. D.
   c=\frac{a+b}{2}

Answer 1

B
分析：先将方程化为[（b-c）x-（a-b）]（x-1）=0的形式，再根据方程有两个相等的实数根可求出x的值，再将x的值代入（b-c）x-（a-b）=0中即可得出a、b、c之间的关系．
解答：∵原方程可化为[（b-c）x-（a-b）]（x-1）=0，
∴（b-c）x-（a-b）=0，x-1=0，
∴x₁=1，x₂=，
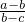
∵关于x的一元二次方程（b-c）x²+（a-b）x+c-a=0（b≠c）有两个相等的实数根，
∴x₁=x₂=1，
∴b-c=a-b，即a-2b+c=0．
∴b=．
故选：B．
点评：本题考查了一元二次方程ax²+bx+c=0（a≠0，a，b，c为常数）的根的判别式△=b²-4ac．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．同时考查了一元二次不等式的解法．
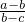