
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,α),B(b,α),且α、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.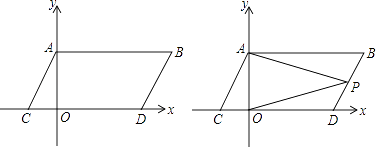
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合) ![]() 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由.
【答案】
(1)
解:∵(a﹣2)2+|b﹣4|=0,
∴a=2,b=4,
∴A(0,2),B(4,2).
∵将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,
∴C(﹣1,0),D(3,0).
∴S四边形ABDC=AB×OA=4×2=8
(2)
解:在y轴上存在一点M,使S△MCD=S四边形ABCD.设M坐标为(0,m).
∵S△MCD=S四边形ABDC,
∴ ![]() ×4|m|=8,
×4|m|=8,
∴2|m|=8,
解得m=±4.
∴M(0,4)或(0,﹣4)
(3)
解:当点P在BD上移动时, ![]() =1不变,理由如下:
=1不变,理由如下:
过点P作PE∥AB交OA于E.
∵CD由AB平移得到,则CD∥AB,
∴PE∥CD,
∴∠BAP=∠APE,∠DOP=∠OPE,
∴∠BAP+∠DOP=∠APE+∠OPE=∠APO,
∴ ![]() =1.
=1.

【解析】(1)先由非负数性质求出a=2,b=4,再根据平移规律,得出点C,D的坐标,然后根据四边形ABDC的面积=AB×OA即可求解;(2)存在.设M坐标为(0,m),根据S△PAB=S四边形ABDC , 列出方程求出m的值,即可确定M点坐标;(3)过P点作PE∥AB交OC与E点,根据平行线的性质得∠BAP+∠DOP=∠APE+∠OPE=∠APO,故比值为1.
【考点精析】本题主要考查了平行线的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是边长为4的正方形,点P从点O沿边OA向点A运动,每秒运动1个单位.连结CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点E作EF∥OA,交OB于点F,连结FD、BE,设点P运动的时间为![]()
![]() .
.
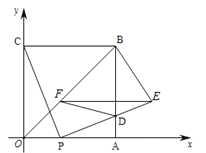
(1)点E的坐标为 (用含![]() 的代数式表示);
的代数式表示);
(2)试判断线段EF的长度是否随点P的运动变化而改变?并说明理由;
(3)当![]() 为何值时,四边形BEDF的面积为
为何值时,四边形BEDF的面积为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
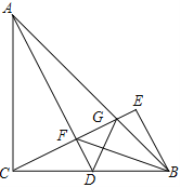
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点D为BC的中点,点E与点C关于直线AD对称,CE与AD、AB分别交于点F、G,连接BE、BF、GD
求证:(1) △BEF为等腰直角三角形 ;(2) ∠ADC=∠BDG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大众创业,万众创新,据不完全统计,2015年毕业的大学生中创业人数已经达到7490000人,将7490000这个数据用科学记数法表示为( )
A.7.49×107
B.7.49×106
C.74.9×106
D.0.749×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com