
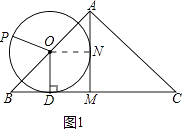
【题目】如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N. 
(1)求证:AN=BD;
(2)填空:点P是⊙O上的一个动点, ①若AB=4,连结OC,则PC的最大值是;
②当∠BOP=时,以O,D,B,P为顶点四边形是平行四边形.
【答案】
(1)证明:如图1中,连接ON.
∵AM是⊙O的切线,
∴ON⊥AM,
∵OD⊥BC,AM⊥BC,
∴∠ODM=∠ONM=∠DMN=90°,
∴四边形ODMN是矩形,
∵OD=ON,
∴四边形ODMN是正方形,
∴OD=ON=DM=MN,
∵OA=OB,OD∥AM,ON∥BM,
∴BD=DM,AN=MN,
∴BD=AN
(2)2 ![]() +
+ ![]() ;45°或135°
;45°或135°
【解析】解:(2)①如图2中,连接OC、PC. 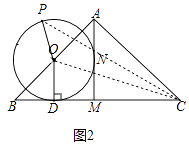
∵PC≤OC+OP,
∴当点P在CO的延长线时,P、O、C共线时,PC的值最大,最大值为OC+OP.
由(1)可知,BM=AM,∠AMB=90°,
∴∠B=45°,
∵AB=AC=4,
∴△ABC是等腰直角三角形,BM=AM=MC=2 ![]() ,OP=OD=BD=DM=
,OP=OD=BD=DM= ![]() ,
,
∴OA=2,OC= ![]() =2
=2 ![]() ,
,
∴PC的最大值为2 ![]() +
+ ![]() ;②如图3中,
;②如图3中,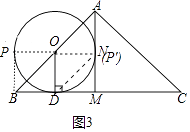
由题意以O,D,B,P为顶点四边形是平行四边形
当OB为对角线时,OP∥BD,可得∠BOP=∠ABC=45°,
当OB为边时,OP′∥BC,可得∠BOP′=180°﹣∠ABC=135°.
综上所述,当∠POB=45°或135°时,以O,D,B,P为顶点四边形是平行四边形;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在下列平面直角坐标系中画出函数y1=-x+3,y2=3x-4的图象.观察图象,回答下列问题:
(1)当x取何值时,y1=y2?
(2)当x取何值时,y1>y2?
(3)当x取何值时,y1<y2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)观察猜想:如图(1),当点D在线段BC上时,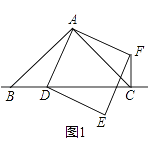
①BC与CF的位置关系是:;
②BC、CD、CF之间的数量关系为:(将结论直接写在横线上)
(2)数学思考:如图(2),当点D在线段CB的延长线上时,上述①、②中的结论是否仍然成立?若成立,请给予证明,若不成立,请你写出正确结论再给予证明.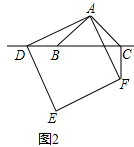
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年11月13日巴基斯坦瓜达尔港正式开港,此港成为我国“一带一路”必展战略上的一颗璀璨的明星,某大型远洋运输集团有三种型号的远洋货轮,每种型号的货轮载重量和盈利情况如下表所示:
甲 | 乙 | 丙 | |
平均货轮载重的吨数(万吨) | 10 | 5 | 7.5 |
平均每吨货物可获例如(百元) | 5 | 3.6 | 4 |
(1)若用乙、丙两种型号的货轮共8艘,将55万吨的货物运送到瓜达尔港,问乙、丙两种型号的货轮各多少艘?
(2)集团计划未来用三种型号的货轮共20艘装运180万吨的货物到国内,并且乙、丙两种型号的货轮数量之和不超过甲型货轮的数量,如果设丙型货轮有m艘,则甲型货轮有艘,乙型货轮有艘(用含有m的式子表示),那么如何安排装运,可使集团获得最大利润?最大利润的多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长为a宽为b的铁板(a>b),从四个角截去四个边长为x的小正方形 ![]() ,做成一个无盖的盒子,用代数式表示:
,做成一个无盖的盒子,用代数式表示:
(1)无盖盒子的外表面积;(用两种方法)
(2)无盖盒子的容积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1 , 点O2 , 点O3…,则O10的坐标是( )
A.(16+4π,0)
B.(14+4π,2)
C.(14+3π,2)
D.(12+3π,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,过B作BE⊥AD交AD于F,交AC于E.
(1)求证:△ABE为等腰三角形;
(2)已知AC=11,AB=6,求BD长.
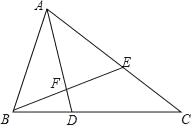
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,AB的垂直平分线交AC于点N,交BC的延长线于点M,∠A=40°.
(1)求∠NMB的大小.
(2)如果将(1)中的∠A的度数改为70°,其余条件不变,再求∠NMB的大小.
(3)你认为存在什么样的规律?试用一句话说明.(请同学们自己画图)
(4)将(1)中的∠A改为钝角,对这个问题规律的认识是否需要加以修改?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm. 
(1)当∠AOB=20°时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=20°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到0.01cm) (参考数据:sin10°≈0.174,cos10°≈0.985,sin20°≈0.342,cos20°≈0.940)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com