
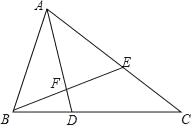
【题目】如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,过B作BE⊥AD交AD于F,交AC于E.
(1)求证:△ABE为等腰三角形;
(2)已知AC=11,AB=6,求BD长.
【答案】(1)详见解析;(2)5.
【解析】试题分析:(1)由垂直的定义得到![]() 由角平分线的定义得到∠EAF=∠BAF,根据三角形的内角和得到∠AEF=∠ABF,得到AE=AB,于是得到结论;
由角平分线的定义得到∠EAF=∠BAF,根据三角形的内角和得到∠AEF=∠ABF,得到AE=AB,于是得到结论;
(2)连接DE,根据等腰三角形的性质得到AD垂直平分BE,得到BD=ED,由等腰三角形的性质得到∠DEF=∠DBF,等量代换得到∠AED=∠ABD,于是得到结论.
试题解析:(1)证明:∵BE⊥AD,
![]()
又∵AD平分∠BAC,
∴∠EAF=∠BAF,
又∵在△AEF和△ABF中
![]()
∴∠AEF=∠ABF,
∴AE=AB,
∴△ABE为等腰三角形;
(2)连接DE,
∵AE=AB,AD平分∠BAC,
∴AD垂直平分BE,
∴BD=ED,
∴∠DEF=∠DBF,
∵∠AEF=∠ABF,
∴∠AED=∠ABD,
又∵∠ABC=2∠C,
∴∠AED=2∠C,
又∵△CED中,∠AED=∠C+∠EDC,
∴∠C=∠EDC,
∴EC=ED,
∴CE=BD.
∴BD=CE=ACAE=ACAB=116=5.



科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( ) 
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=﹣x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(﹣4,5),并与y轴交于点C,抛物线的对称轴为直线x=﹣1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=﹣1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N. 
(1)求证:AN=BD;
(2)填空:点P是⊙O上的一个动点, ①若AB=4,连结OC,则PC的最大值是;
②当∠BOP=时,以O,D,B,P为顶点四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在暑假社会实践活动中,以每千克![]() 元的价格从批发市场购进若干千克西瓜市场上去销售,在销售了
元的价格从批发市场购进若干千克西瓜市场上去销售,在销售了![]() 千克之后,余下的打折全部售完.销售金额
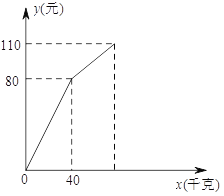
千克之后,余下的打折全部售完.销售金额![]() (元)售出西瓜的千克数
(元)售出西瓜的千克数![]() (千克)之间的关系如图所示.请你根据图像提供的信息完成以下问题:
(千克)之间的关系如图所示.请你根据图像提供的信息完成以下问题:
(![]() )求降价前销售金额
)求降价前销售金额![]() (元)与售出西瓜
(元)与售出西瓜![]() (千克)之间的关系;
(千克)之间的关系;
(![]() )小明这次社会实践活动赚了多少钱?
)小明这次社会实践活动赚了多少钱?
(![]() )若要使这次活动赚
)若要使这次活动赚![]() 元钱,问余下的西瓜应打几折销售完?
元钱,问余下的西瓜应打几折销售完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形ABC有一外接圆,其中∠B=90°,AB>BC,今欲在 ![]() 上找一点P,使得
上找一点P,使得 ![]() =
= ![]() ,以下是甲、乙两人的作法: 甲:⑴取AB中点D
,以下是甲、乙两人的作法: 甲:⑴取AB中点D
⑵过D作直线AC的平行线,交 ![]() 于P,则P即为所求
于P,则P即为所求
乙:⑴取AC中点E
⑵过E作直线AB的平行线,交 ![]() 于P,则P即为所求
于P,则P即为所求
对于甲、乙两人的作法,下列判断何者正确?( )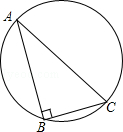
A.两人皆正确
B.两人皆错误
C.甲正确,乙错误C
D.甲错误,乙正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com