
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( ) 
A.2
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵OP平分∠AOB,∠AOB=60°, ∴∠AOP=∠COP=30°,
∵CP∥OA,
∴∠AOP=∠CPO,
∴∠COP=∠CPO,
∴OC=CP=2,
∵∠PCE=∠AOB=60°,PE⊥OB,
∴∠CPE=30°,
∴CE= ![]() CP=1,
CP=1,
∴PE= ![]() =
= ![]() ,
,
∴OP=2PE=2 ![]() ,
,
∵PD⊥OA,点M是OP的中点,
∴DM= ![]() OP=
OP= ![]() .
.
故选:C.
由OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,易得△OCP是等腰三角形,∠COP=30°,又由含30°角的直角三角形的性质,即可求得PE的值,继而求得OP的长,然后由直角三角形斜边上的中线等于斜边的一半,即可求得DM的长.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知△ABC是等腰三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
(1)试猜想线段BG和AE的数量关系;
(2)如图②,将正方形DEFG绕点D按逆时针方向旋转α(0°<α≤90°),判断(1)中的结论是否仍然成立,证明你的结论.

(3)若BC=DE=2,在(2)的旋转过程中,求线段AE长的最大值和最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为a的正方形上剪去一个边长为b的小正方形(a>b),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )

A. a2-b2=(a+b)(a-b) B. (a+b)2=a2+2ab+b2
C. (a-b)2=a2-2ab+b2 D. a2-ab=a(a-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
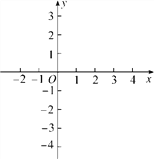
【题目】在下列平面直角坐标系中画出函数y1=-x+3,y2=3x-4的图象.观察图象,回答下列问题:
(1)当x取何值时,y1=y2?
(2)当x取何值时,y1>y2?
(3)当x取何值时,y1<y2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OD平分∠AOC,∠DOE=90°,则以下结论正确的个数是( )
①∠AOD与∠BOE互为余角;②∠AOD=∠COE;③∠BOE=∠COE;④∠DOC与∠DOB互补.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠AOM= 度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)观察猜想:如图(1),当点D在线段BC上时,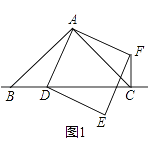
①BC与CF的位置关系是:;
②BC、CD、CF之间的数量关系为:(将结论直接写在横线上)
(2)数学思考:如图(2),当点D在线段CB的延长线上时,上述①、②中的结论是否仍然成立?若成立,请给予证明,若不成立,请你写出正确结论再给予证明.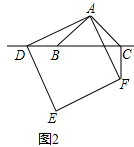
查看答案和解析>>
科目:初中数学 来源: 题型:
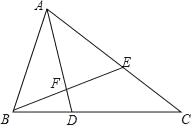
【题目】如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,过B作BE⊥AD交AD于F,交AC于E.
(1)求证:△ABE为等腰三角形;
(2)已知AC=11,AB=6,求BD长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com