
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠AOM= 度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 .
【答案】(1)120;(2)∠AOM﹣∠NOC=30°,理由参见解析;(3)6或24秒.
【解析】
试题分析:(1)由角平分线意义可得∠BOM=120°÷2=60°,根据平角的意义可算出∠AOM的度数;(2)如图3,∠AOM转化成∠MON-∠AON,∠NOC转化成∠AOC-∠AON,则∠AOM﹣∠NOC=(∠MON-∠AON)-(∠AOC-∠AON),即等于∠MON-∠AON-∠AOC+∠AON=∠MON-∠AOC=90-60=30度,从而推出∠AOM与∠NOC之间的数量关系;(3)若直线ON恰好平分∠AOC,当逆时针旋转60°时,ON平分∠AOC,或当逆时针旋转240°时,ON平分∠AOC,分别除以10,即为所求的旋转时间.
试题解析:(1)由题意可知:OM恰好平分∠BOC,∴∠BOM=120°÷2=60°,∴∠AOM=180°﹣60°=120°; (2)如图3,∵∠BOC=120°,∴∠A0C=60°,∠AOM转化成∠MON-∠AON,∠NOC转化成∠AOC-∠AON,∵∠AON=90°﹣∠AOM=60°﹣∠NOC,∴∠AOM﹣∠NOC=30°;(3)设三角板绕点O旋转的时间是x秒,∵∠BOC=120°,∴∠AOC=60°,当逆时针旋转60°或逆时针旋转240°时 ON平分∠AOC, 于是可列10x=60或10x=240,∴x=6或x=24,即此时三角板绕点O旋转的时间是6秒或24秒.故答案为:6秒或24秒.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为 .
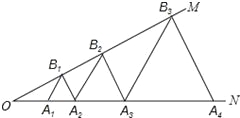
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年冬天受寒潮影响,淘宝上的电热取暖器销售火爆.某电商销售每台成本价分别为200元、170元的A、B两种型号的电热取暖器,下表是近两天的销售情况:
销售时段 | |||
销售数量 | |||
A种型号 | B种型号 | 销售收入 | |
第一天 | 3台 | 5台 | 1800元 |
第二天 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电热取暖器的销售单价;
(2)若该电商准备用不多于5400元的金额再采购这两种型号的电热取暖器共30台,问A种型号的电热取暖器最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( ) 
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个水池深3m,池中水深1m,现在要把水池中的水注满,每注水1h,池中的水深增加0.4m.
(1)写出池中的水深y(m)与注水时间x(h)之间的函数关系式.
(2)求自变量的取值范围.
(3)画出这个函数的图像.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为 . 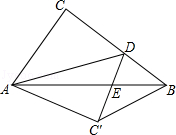
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读材料】
小明在学习二次根式时,发现一些含根号的式子可以化成另一式子的平方.如:
5+2![]() =(2+3)+2
=(2+3)+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() =(
=(![]() )2;
)2;
8+2![]() =(3+5)+2
=(3+5)+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() =(
=(![]() )2.
)2.
【类比归纳】
(1)请你仿照小明的方法将9+2![]() 化成一个式子的平方;
化成一个式子的平方;
(2)将下列等式补充完整:a+b+2![]() =( )2(a≥0,b≥0),并证明这个等式;
=( )2(a≥0,b≥0),并证明这个等式;
【变式探究】
(3)若a+2![]() =(
=(![]() )2,且a,m,n均为正整数,则a= .
)2,且a,m,n均为正整数,则a= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com