练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一个水池深3m,池中水深1m,现在要把水池中的水注满，每注水1h,池中的水深增加0.4m.

    （1）写出池中的水深y(m)与注水时间x(h)之间的函数关系式.

    （2）求自变量的取值范围.

    （3）画出这个函数的图像.

    【答案】（1）y=1+0.4x；（2）;（3）见解析.

    【解析】试题分析:(1)根据水深=原来的水深1+注水的时间乘以水深增加的速度0.4米每小时可求出函数关系式,(2)根据y的取值范围是,代入(1)中函数关系式可求出自变量的取值范围,(3)通过列表,描点,连线即可求解.

    试题解析: (1)水深y=原来的水深1+注水的时间x乘以水深增加的速度0.4米每小时,所以y=0.4x+1,(2)由于水池最少深1米,最多深3米,也就是y的取值范围是,

    x=（y-1）/0.4,所以x的取值范围是.

    (3)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

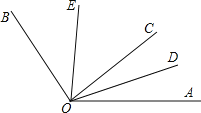
    【题目】如图，∠AOB=120°，OC是∠AOB内部任意一条射线，OD、OE分别是∠AOC、∠BOC的角平分线，下列叙述正确的是（　　）

    A. ∠DOE的度数不能确定 B. ∠AOD=∠EOC

    C. ∠AOD+∠BOE=60° D. ∠BOE=2∠COD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】决心试一试，请阅读下列材料：计算：

    解法一：原式=

    =

    =

    解法二：原式=

    =

    =

    =

    解法三：原式的倒数为：

    =

    =﹣20+3﹣5+12

    =﹣10

    故原式 =

    上述得出的结果不同，肯定有错误的解法，你认为解法 是错误的，在正确的解法中，你认为解法 最简捷．然后请解答下列问题,计算：.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知线段AB和CD的公共部分BD=AB= CD，线段AB、CD的中点E，F之间距离是10cm，求AB，CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点O为直线AB上一点，过O点作射线OC，使∠BOC=120°，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．

    （1）如图2，将图1中的三角板绕点O逆时针旋转，使边OM在∠BOC的内部，且OM恰好平分∠BOC．此时∠AOM= 度；

    （2）如图3，继续将图2中的三角板绕点O按逆时针方向旋转，使得ON在∠AOC的内部．试探究∠AOM与∠NOC之间满足什么等量关系，并说明理由；

    （3）将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周，在旋转的过程中，若直线ON恰好平分∠AOC，则此时三角板绕点O旋转的时间是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是生活中常见的月历的示意图，请结合图示回答下列问题．

    一

    二

    三

    四

    五

    六

    日

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    (1)如图是另一个月的月历，a表示该月中某一天，b，c，d是该月中其他3天，b，c，d分别与a的关系：b＝________；c＝________；d＝________(用含a的代数式填空)．

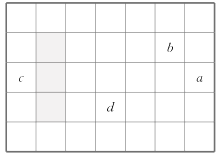
    (2)用一个长方形框圈出月历中的三个数(如 图中的阴影)，若这三个数之和等于51，则这三个数分别是多少？

    (3)这样圈出的三个数的和可能是64吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着柴静纪录片《穹顶之下》的播出，全社会对空气污染问题越来越重视，空气净化器的销量也大增，商社电器从厂家购进了A，B两种型号的空气净化器，已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元，用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同．
    （1）求一台A型空气净化器和一台B型空气净化器的进价各为多少元？
    （2）在销售过程中，A型空气净化器因为净化能力强，噪音小而更受消费者的欢迎．为了增大B型空气净化器的销量，商社电器决定对B型空气净化器进行降价销售，经市场调查，当B型空气净化器的售价为1800元时，每天可卖出4台，在此基础上，售价每降低50元，每天将多售出1台，如果每天商社电器销售B型空气净化器的利润为3200元，请问商社电器应将B型空气净化器的售价定为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】按图中方式用火柴棒搭正方形

    ①搭1个正方形需要 根火柴棒；

    ②搭2个正方形需要 根火柴棒，搭3个正方形需要 根火柴棒；

    ③搭10个这样的正方形需要多少根火柴棒；

    ④搭100个这样的正方形需要多少根火柴棒？

    ⑤如果用x表示所搭正方形的个数，那么搭x个这样的正方形需要多少根火柴棒？与同伴交流。

    ⑥根据你的计算方法，搭200个这样的正方形需要多少根火柴棒？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解并完成下面问题：

    我们知道，任意一个正整数都可以进行这样的因式分解：（是正整数），在的所有这种分解中，如果两因数之差的绝对值最小，我们就称是的最佳分解．并规定：

    （其中）．例如：可以分解成，或，因为，所以是的最佳分解，所以．

    （）如果一个正整数是另外一个正整数的平方，我们称正整数是完全平方数，若是一个完全平方数，求的值；

    （）如果一个两位正整数，交换其个位数字与十位数字得到的新两位数减去原数所得的差为，那么我们称这个两位正整数为“吉祥数”，求符合条件的所有“吉祥数”；

    （）在（）中的所有“吉祥数”中，求的最小值．

    查看答案和解析>>

    同步练习册答案