
【题目】如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( )
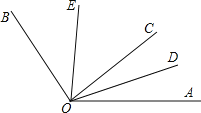
A. ∠DOE的度数不能确定 B. ∠AOD=![]() ∠EOC
∠EOC
C. ∠AOD+∠BOE=60° D. ∠BOE=2∠COD
科目:初中数学 来源: 题型:
【题目】某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成下图.请根据图像回答问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多少时间?
(2)第三天12时这头骆驼的体温约是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
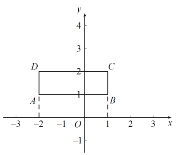
【题目】如图,在平面直角坐标系xOy中,长方形ABCD的四个顶点分别为(1,1),(1,2),(-2,2),(-2,1).对该长方形及其内部的每一个点都进行如下操作:把每个点的横坐标都乘以同一个实数a,纵坐标都乘以3,再将得到的点向右平移m(m>0)个单位,向下平移2个单位,得到长方形ABCD及其内部的点,其中点A,B,C,D的对应点分别为A,B,C,D.
(1)点A的横坐标为__________(用含a,m的式子表示).
(2)点A的坐标为(3,1),点C的坐标为(-3,4),
①求a,m的值;
②若对长方形ABCD内部(不包括边界)的点E(0,y)进行上述操作后,得到的对应点E仍然在长方形ABCD内部(不包括边界),求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与直线y= ![]() x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
(1)求抛物线的解析式;
(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.
(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=x+1的图象与y轴交于点A,一次函数y2=kx+b的图象经过点B(0,3),且分别与x轴及y1=x+1的图象交于点C,D,点D的横坐标为![]() .
.
(1)求k,b的值;
(2)当x_____时,y2>0;
(3)若在一次函数y1=x+1的图象上有一点E(![]() ,n),将点E向右平移2个单位后,得对应点E',判断点E'是否在一次函数y2=kx+b的图象上.
,n),将点E向右平移2个单位后,得对应点E',判断点E'是否在一次函数y2=kx+b的图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+b的顶点坐标为(0,﹣1),且经过点A(﹣2,0). 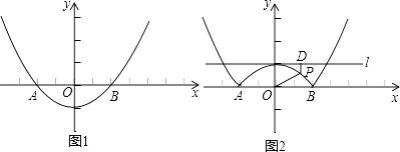
(1)求抛物线的解析式;
(2)若将抛物线y=ax2+b中在x轴下方的图象沿x轴翻折到x轴上方,x轴上方的图象保持不变,就得到了函数y=|ax2+b|图象上的任意一点P,直线l是经过(0,1)且平行与x轴的直线,过点P作直线l的垂线,垂足为D,猜想并探究:PO与PD的差是否为定值?如果是,请求出此定值;如果不是,请说明理由. (注:在解题过程中,如果你觉得有困难,可以阅读下面的材料)
附阅读材料:
① 在平面直角坐标系中,若A、B两点的坐标分别为A(x1 , y1),B(x2 , y2),则A,B两点间的距离为|AB|= ![]() ,这个公式叫两点间距离公式.
,这个公式叫两点间距离公式.
例如:已知A,B两点的坐标分别为(﹣1,2),(2,﹣2),则A,B两点间的距离为|AB|= ![]() =5.
=5.
② 因式分解:x4+2x2y2+y4=(x2+y2)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个水池深3m,池中水深1m,现在要把水池中的水注满,每注水1h,池中的水深增加0.4m.
(1)写出池中的水深y(m)与注水时间x(h)之间的函数关系式.
(2)求自变量的取值范围.
(3)画出这个函数的图像.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com