
����Ŀ����ͼ��������y=x2+bx+c��ֱ��y= ![]() x��3����A��B���㣬���е�A��y���ϣ���B����Ϊ����4����5������PΪy��������������һ���㣬����P��PC��x���ڵ�C����AB�ڵ�D��
x��3����A��B���㣬���е�A��y���ϣ���B����Ϊ����4����5������PΪy��������������һ���㣬����P��PC��x���ڵ�C����AB�ڵ�D��
��1���������ߵĽ���ʽ��
��2����O��A��P��DΪ�����ƽ���ı����Ƿ���ڣ�����ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
��3������P�˶���ֱ��AB�·�ijһ��ʱ������P��PM��AB������ΪM������PAʹ��PAMΪ����ֱ�������Σ���ֱ��д����ʱ��P�����꣮
���𰸡�
��1��
�⣺��ֱ��y= ![]() x��3����A��B���㣬���е�A��y���ϣ�
x��3����A��B���㣬���е�A��y���ϣ�
��A��0����3����
��B����4����5����
�� ![]() ��
��
�� 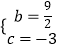 ��
��
�������߽���ʽΪy=x2+ ![]() x��3
x��3
��2��
�⣺���ڣ�
��P��m��m2+ ![]() m��3������m��0����
m��3������m��0����
��D��m�� ![]() m��3����
m��3����
��PD=|m2+4m|
��PD��AO��
�൱PD=OA=3���ʴ�����O��A��P��DΪ�����ƽ���ı��Σ�
��|m2+4m|=3��
�� ��m2+4m=3ʱ��
��m1=��2�� ![]() ��m2=��2+
��m2=��2+ ![]() ���ᣩ��
���ᣩ��
��m2+ ![]() m��3=��1��
m��3=��1�� ![]() ��
��
��P����2�� ![]() ����1��
����1�� ![]() ����
����
�ڵ�m2+4m=��3ʱ��
��m1=��1��m2=��3��
��m1=��1��
��m2+ ![]() m��3=��
m��3=�� ![]() ��
��
��P����1���� ![]() ����
����
��m2=��3��
��m2+ ![]() m��3=��
m��3=�� ![]() ��
��
��P����3���� ![]() ����
����
���P����������2�� ![]() ����1��
����1�� ![]() ��������1����
��������1���� ![]() ��������3����
��������3���� ![]() ��
��
��3��
�⣺����һ����ͼ��
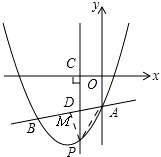
�ߡ�PAMΪ����ֱ�������Σ�
���BAP=45�㣬
��ֱ��AP���Կ�����ֱ��AB�Ƶ�A��ʱ����ת45�����ã�
��ֱ��AP����ʽΪy=kx��3��
��ֱ��AB����ʽΪy= ![]() x��3��
x��3��
��k= ![]() =3��
=3��
��ֱ��AP����ʽΪy=3x��3��
���� 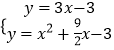 ��
��
��x1=0���ᣩx2=�� ![]()
��x=�� ![]() ʱ��y=��
ʱ��y=�� ![]() ��
��
��P���� ![]() ����
���� ![]() ����
����
����������ͼ��
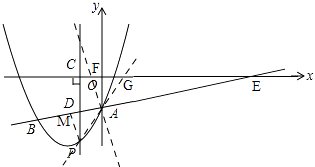
��ֱ��AB����ʽΪy= ![]() x��3��
x��3��
��ֱ��AB��x��Ľ�������ΪE��6��0����
����A��AF��AB��x���ڵ�F��
��A��0����3����
��ֱ��AF����ʽΪy=��2x��3��
��ֱ��AF��x��Ľ���ΪF���� ![]() ��0����
��0����
��AE=3 ![]() ��AF=
��AF= ![]() ��
��
����A����EAF�Ľ�ƽ���߽�x���ڵ�G��������������ڵ�P������P��PM��AB��
���EAG=45�㣬
���BAP=45�㣬
������PAMΪ����ֱ�������Σ�
���G��m��0����
��EG=6��m��FG=m+ ![]() ��
��
���ݽ�ƽ���߶����ã� ![]() ��
��
�� ![]() ��
��
��m=1��
��G��1��0����
��ֱ��AG����ʽΪy=3x��3�٣�
�������߽���ʽΪy=x2+ ![]() x��3�ڣ�
x��3�ڣ�
�����٢ڵã�x=0���ᣩ��x=�� ![]() ��
��
��y=�� ![]() ��
��
��P���� ![]() ����
���� ![]() ��
��
����������1����ȷ������A���꣬Ȼ���ô���ϵ�����������߽���ʽ����2����ȷ����PD=|m2+4m|����PD=OA=3���ʴ�����O��A��P��DΪ�����ƽ���ı��Σ��õ�|m2+4m|=3������������������ۼ��㼴�ɣ���3���ɡ�PAMΪ����ֱ�������Σ��õ���BAP=45�㣬�Ӷ����ֱ��AP�Ľ���ʽ��������ֱ��AP�������ߵĽ������꼴�ɣ�


 ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
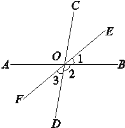
����Ŀ����ͼ��ֱ��AB��CD���ڵ�O���ҡ�BOC��80�㣬OEƽ�֡�BOC��OFΪOE�ķ����ӳ��ߣ�
(1)���2�͡�3�Ķ�����
(2)OFƽ�֡�AOD��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С���ļ�λ��һ���ϱ�����ĺ���MN�Ķ���A����ijһ��С���Ӽҳ�������ƫ��30�㷽����60 m����ӱ�B��ȡˮ��Ȼ������һ������80 m����˵�C����ˮ������ص���������100 m�ص���A������С���ںӱ�B��ȡˮ�������ĸ��������ߵģ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������1���ಿ��ͬѧ����һ������Ϊ�����ʺ��Լ��Ŀ�ǰ��ѹ��ʽ���ĵ������ռ��������ݺ���ʦ����ѹ��ʽ��Ϊ���࣬��������ͼ1��ͼ2������������ͳ��ͼ�������ͼ�е���Ϣ����������⣮ 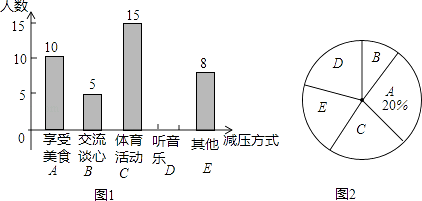
��1��������1������ܵ����ͬѧ���ж�������
��2����ȫ����ͳ��ͼ������������ͳ��ͼ�еġ������C������Ӧ��Բ�ĽǶ�����
��3����ϲ��������̸�ġ���5��ͬѧ������������������Ů������ʦ���5��ͬѧ����ѡ����ͬѧ���н�����ֱ��д��ѡȡ������ͬѧ����Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=120�㣬OC����AOB�ڲ�����һ�����ߣ�OD��OE�ֱ�����AOC����BOC�Ľ�ƽ���ߣ�����������ȷ���ǣ�������
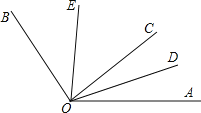
A. ��DOE�Ķ�������ȷ�� B. ��AOD=![]() ��EOC
��EOC
C. ��AOD+��BOE=60�� D. ��BOE=2��COD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ڳ�����ABCD����AB��12 cm��BC��6 cm.��P��AB�ߴӵ�A��ʼ���B��2 cm/s���ٶ��ƶ�����Q��DA�ߴӵ�D��ʼ���A��1 cm/s���ٶ��ƶ���
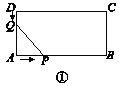
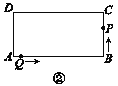
���P��Qͬʱ��������t(s)��ʾ�ƶ���ʱ�䣮
�����֣� DQ��________cm��AP��________cm.(�ú�t�Ĵ���ʽ��ʾ)
����չ��(1)��ͼ������t��________sʱ���߶�AQ���߶�AP��ȣ�
(2)��ͼ������P��Q�ֱ�B��A������˶�����P�����C��ֹͣ�˶���
��tΪ��ֵʱ��AQ��![]() CP?
CP?
��̽��������P��Q�ֱ��B��A���������A��B��C��D��A�ķ����˶�������P���Q��һ������ʱ����ֱ��д���������λ�ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����BAC=45�㣬AD��BC�ڵ�D��BE��AC�ڵ�E������AD���ڵ�F��G�DZ�AB���е㣬����EG��AD�ڵ�H��
��1����֤����AEF�ա�BEC��
��2����֤��CD=![]() AF��
AF��
��3����BD=2����AH�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����OD��ֱ��AC�ڵ�E���ҽ���O�ڵ�D������D����O��������BA���ӳ����ཻ�ڵ�F�����н��۲�һ����ȷ���ǣ� �� 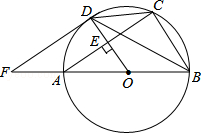
A.��CDB=��BFD
B.��BAC�ס�OFD
C.DF��AC
D.OD=BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������г�����������ʾ��ͼ������ͼʾ�ش��������⣮
һ | �� | �� | �� | �� | �� | �� |
1 | 2 | 3 | 4 | 5 | ||
6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 | 14 | 15 | 16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 |
(1)��ͼ����һ���µ�������a��ʾ������ijһ����b��c��d�Ǹ���������3����b��c��d�ֱ���a�Ĺ�ϵ��b��________��c��________��d��________(�ú�a�Ĵ���ʽ���)��
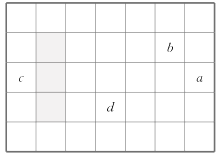
(2)��һ�������ο�Ȧ�������е�������(�� ͼ�е���Ӱ)������������֮�͵���51�������������ֱ��Ƕ��٣�
(3)����Ȧ�����������ĺͿ�����64��Ϊʲô��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com