练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AB=AC，∠BAC=45°，AD⊥BC于点D，BE⊥AC于点E，且与AD交于点F．G是边AB的中点，连接EG交AD于点H．

    （1）求证：△AEF≌△BEC；

    （2）求证：CD=AF；

    （3）若BD=2，求AH的长．

    【答案】（1）（2）见解析；（3）

    【解析】试题分析：(1)根据及知证得结合 可证得答案;
    (2)由≌，知,根据知即可得证.
    (3)连接BH,根据垂直平分线的性质和勾股定理即可得出答案.

    试题解析：（1）∵

    ∴

    ∵

    ∴

    ∴

    在和中，

    ∵

    ∴≌（ASA）；

    （2）∵≌，

    ∴

    ∵

    ∴

    ∴

    即

    （3）连接BH，

    ∵

    ∴

    ∵ G是边AB的中点，

    ∴EG垂直平分AB，

    ∴

    ∴∠5=∠6=22.5°，

    ∴

    ∵

    ∴

    ∴

    在中，由勾股定理得；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下图是由一些火柴棒搭成的图案：

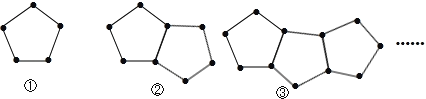
    （1）摆第①个图案用 根火柴棒，摆第②个图案用 根火柴棒，摆第③个图案用 根火柴棒．

    （2）按照这种方式摆下去，摆第n个图案用多少根火柴棒？

    （3）计算一下摆121根火柴棒时，是第几个图案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

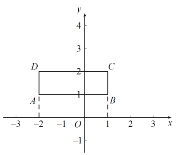
    【题目】如图，在平面直角坐标系xOy中，长方形ABCD的四个顶点分别为（1，1），（1，2），（-2，2），（-2，1）.对该长方形及其内部的每一个点都进行如下操作：把每个点的横坐标都乘以同一个实数a，纵坐标都乘以3，再将得到的点向右平移m（m＞0）个单位，向下平移2个单位，得到长方形ABCD及其内部的点，其中点A，B，C，D的对应点分别为A，B，C，D.

    （1）点A的横坐标为__________（用含a,m的式子表示）.

    （2）点A的坐标为（3，1），点C的坐标为（-3，4），

    ①求a，m的值；

    ②若对长方形ABCD内部（不包括边界）的点E(0，y)进行上述操作后，得到的对应点E仍然在长方形ABCD内部（不包括边界），求y的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=x2+bx+c与直线y= x﹣3交于A、B两点，其中点A在y轴上，点B坐标为（﹣4，﹣5），点P为y轴左侧的抛物线上一动点，过点P作PC⊥x轴于点C，交AB于点D．

    （1）求抛物线的解析式；
    （2）以O，A，P，D为顶点的平行四边形是否存在？如存在，求点P的坐标；若不存在，说明理由．
    （3）当点P运动到直线AB下方某一处时，过点P作PM⊥AB，垂足为M，连接PA使△PAM为等腰直角三角形，请直接写出此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知一次函数y1=x+1的图象与y轴交于点A，一次函数y2=kx+b的图象经过点B（0，3），且分别与x轴及y1=x+1的图象交于点C，D，点D的横坐标为．

    （1）求k，b的值；

    （2）当x_____时，y2＞0；

    （3）若在一次函数y1=x+1的图象上有一点E（，n），将点E向右平移2个单位后，得对应点E'，判断点E'是否在一次函数y2=kx+b的图象上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某化工厂从2008年开始节能减排，控制二氧化硫的排放图，图分别是该厂年二氧化硫排放量单位：吨的两幅不完整的统计图，根据图中信息回答下列问题．

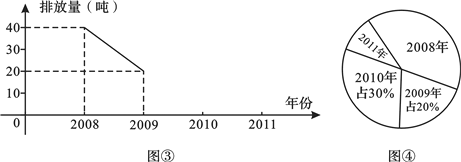
    该厂年二氧化硫排放总量是______ 吨；这四年平均每年二氧化硫排放量是______ 吨

    把图中折线图补充完整．

    年二氧化硫的排放量对应扇形的圆心角是______ 度，2011年二氧化硫的排放量占这四年排放总量的百分比是______ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线y=ax2+b的顶点坐标为（0，﹣1），且经过点A（﹣2，0）．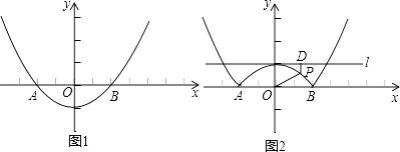
    （1）求抛物线的解析式；
    （2）若将抛物线y=ax2+b中在x轴下方的图象沿x轴翻折到x轴上方，x轴上方的图象保持不变，就得到了函数y=|ax2+b|图象上的任意一点P，直线l是经过（0，1）且平行与x轴的直线，过点P作直线l的垂线，垂足为D，猜想并探究：PO与PD的差是否为定值？如果是，请求出此定值；如果不是，请说明理由． （注：在解题过程中，如果你觉得有困难，可以阅读下面的材料）
    附阅读材料：
    ① 在平面直角坐标系中，若A、B两点的坐标分别为A（x1 ， y1），B（x2 ， y2），则A，B两点间的距离为|AB|= ，这个公式叫两点间距离公式．
    例如：已知A，B两点的坐标分别为（﹣1，2），（2，﹣2），则A，B两点间的距离为|AB|= =5．
    ② 因式分解：x4+2x2y2+y4=（x2+y2）2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

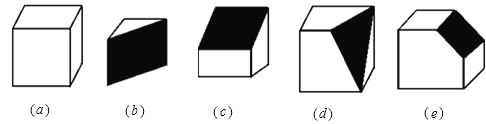
    【题目】（10分）下列图形中，图（a）是正方体木块，把它切去一块，得到如图（b）（c）（d）（e）的木块．

    （1）我们知道，图（a）的正方体木块有8个顶点、12条棱、6个面，请你将图（b）、（c）、（d）、（e）中木块的顶点数、棱数、面数填入下表；

    （2）上表，各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律，请你试写出顶点数x、棱数y、面数z之间的数量关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在下列解题过程的空白处填上适当的内容（推理的理由或数学表达式）

    如图，在△ABC中，已知∠ADE＝∠B，∠1＝∠2，FG⊥AB于点G.

    求证CD⊥AB.

    证明:∵∠ADE＝∠B（已知），

    ∴ （ ），

    ∵ DE∥BC（已证），

    ∴ （ ），

    又∵∠1＝∠2（已知），

    ∴ （ ），

    ∴CD∥FG（ ），

    ∴ （两直线平行同位角相等），

    ∵ FG⊥AB（已知），

    ∴∠FGB＝90°（垂直的定义）.

    即∠CDB＝∠FGB＝90°，

    ∴CD⊥AB. （垂直的定义）.

    查看答案和解析>>

    同步练习册答案