练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

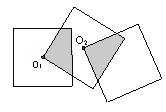
    【题目】如图，三个边长均为2的正方形重叠在一起，O1、O2是其中两个正方形的中心，则阴影部分的面积是 ．

    【答案】2．

    【解析】

    试题分析：根据题意作图，连接O1B，O1C，可得△O1BF≌△O1CG，那么可得阴影部分的面积与正方形面积的关系，同理得出另两个正方形的阴影部分面积与正方形面积的关系，从而得出答案．

    试题解析：连接O1B、O1C，如图：

    ∵∠BO1F+∠FO1C=90°，∠FO1C+∠CO1G=90°，

    ∴∠BO1F=∠CO1G，

    ∵四边形ABCD是正方形，

    ∴∠O1BF=∠O1CG=45°，

    在△O1BF和△O1CG中

    ∴△O1BF≌△O1CG，

    ∴O1、O2两个正方形阴影部分的面积是S正方形，

    同理另外两个正方形阴影部分的面积也是S正方形，

    ∴S阴影部分=S正方形=2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，下列能判定AB∥CD的条件有（ ）个．

    （1）∠B+∠BCD=180°；（2）∠1=∠2；（3）∠3=∠4；（4）∠B=∠5．

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=BC=8，AO=BO，点M是射线CO上的一个动点，∠AOC=60°，则当△ABM为直角三角形时，AM的长为____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设中学生体质健康综合评定成绩为x分，满分为100分，规定：85≤x≤100为A级，75≤x≤85为B级，60≤x≤75为C级，x＜60为D级．现随机抽取福海中学部分学生的综合评定成绩，整理绘制成如下两幅不完整的统计图，请根据图中的信息，解答下列问题：

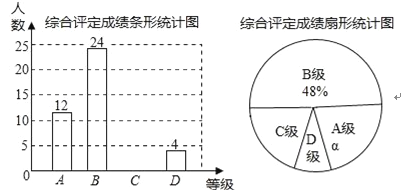
    （1）在这次调查中，一共抽取了 名学生，α= %；

    （2）补全条形统计图；

    （3）扇形统计图中C级对应的圆心角为 度；

    （4）若该校共有2000名学生，请你估计该校D级学生有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，已知△ABC是等腰三角形，∠BAC=90°，点D是BC的中点，作正方形DEFG，使点A、C分别在DG和DE上，连接AE、BG．

    （1）试猜想线段BG和AE的数量关系；

    （2）如图②，将正方形DEFG绕点D按逆时针方向旋转α（0°＜α≤90°），判断（1）中的结论是否仍然成立，证明你的结论．

    (3)若BC=DE=2,在（2）的旋转过程中,求线段AE长的最大值和最小值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠AOB=120°，OC是∠AOB内部任意一条射线，OD、OE分别是∠AOC、∠BOC的角平分线，下列叙述正确的是（　　）

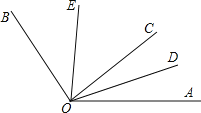
    A. ∠DOE的度数不能确定 B. ∠AOD=∠EOC

    C. ∠AOD+∠BOE=60° D. ∠BOE=2∠COD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：把函数y=bx+a和函数y=ax+b（其中a，b是常数，且a≠0，b≠0）称为一对交换函数，其中一个函数是另一个函数的交换函数．比如，函数y=4x+1是函数y=x+4的交换函数，等等．

    (1)直接写出函数y=2x+1的交换函数；_________________；并直接写出这对交换函数和x轴所围图形的面积为_____________________________；

    (2)若一次函数y=ax+2a和其交换函数与x轴所围图形的面积为3，求a的值．

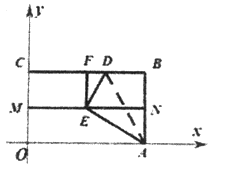
    (3)如图，在平面直角坐标xOy中，矩形OABC中，点C(0， )，M、N分别是线段OC、AB的中点，将△ABD沿着折痕AD翻折，使点B的落点E恰好落在线段MN的中点，点F是线段BC的中点，连接EF，若一次函数和与线段EF始终都有交点，则m的取值范围为_____________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】.某区在实施居民用水额定管理前，对居民生活用水情况进行了调查，下表是通过简单随机抽样获得的50个家庭去年月平均用水量单位：吨，并将调查数据进行如下整理：

    频数分布表

    分组

    划记

    频数

    正正

    11

    19

    合计

    2

    50

    把上面频数分布表和频数分布直方图补充完整；

    从直方图中你能得到什么信息？ 写出两条即可；

    为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按倍价格收费，若要使的家庭收费不受影响，你觉得家庭月均用水量应该定为多少？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点O为直线AB上一点，过O点作射线OC，使∠BOC=120°，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．

    （1）如图2，将图1中的三角板绕点O逆时针旋转，使边OM在∠BOC的内部，且OM恰好平分∠BOC．此时∠AOM= 度；

    （2）如图3，继续将图2中的三角板绕点O按逆时针方向旋转，使得ON在∠AOC的内部．试探究∠AOM与∠NOC之间满足什么等量关系，并说明理由；

    （3）将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周，在旋转的过程中，若直线ON恰好平分∠AOC，则此时三角板绕点O旋转的时间是 ．

    查看答案和解析>>

    同步练习册答案