练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】按图中方式用火柴棒搭正方形

    ①搭1个正方形需要 根火柴棒；

    ②搭2个正方形需要 根火柴棒，搭3个正方形需要 根火柴棒；

    ③搭10个这样的正方形需要多少根火柴棒；

    ④搭100个这样的正方形需要多少根火柴棒？

    ⑤如果用x表示所搭正方形的个数，那么搭x个这样的正方形需要多少根火柴棒？与同伴交流。

    ⑥根据你的计算方法，搭200个这样的正方形需要多少根火柴棒？

    【答案】① 4 ②7 10 ③ 31 ④301 ⑤3x+1 ⑥ 601

    【解析】①有图可知，搭1个正方形需要4根火柴棒；

    ②搭2个正方形需要4＋3＝7根火柴棒，搭3个正方形需要4＋2×3＝10根火柴棒；

    ③搭10个这样的正方形需要4＋9×3＝31根火柴棒；

    ④搭100个这样的正方形需要4＋99×3＝301根火柴棒；

    ⑤搭x个这样的正方形需要4＋（x1）×3＝1＋3x根火柴棒.

    ⑥把x=200代入3x+1中，即可求解.

    ①搭1个正方形需要4根火柴棒；

    ②搭2个需要4＋3×1＝7，搭3个需要4＋3×2＝10；

    ③搭10个需要4＋3×9＝31；

    ④搭100个需要4＋3×99＝301；

    ⑤搭x需要4＋3×（x1）＝3x+1．

    ⑥当x=200时，3x+1=3×200+1=601，即搭200个这样的正方形需要601根火柴棒.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线y=ax2+b的顶点坐标为（0，﹣1），且经过点A（﹣2，0）．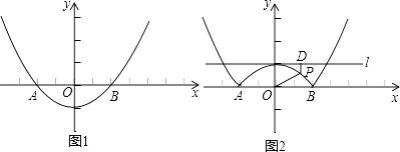
    （1）求抛物线的解析式；
    （2）若将抛物线y=ax2+b中在x轴下方的图象沿x轴翻折到x轴上方，x轴上方的图象保持不变，就得到了函数y=|ax2+b|图象上的任意一点P，直线l是经过（0，1）且平行与x轴的直线，过点P作直线l的垂线，垂足为D，猜想并探究：PO与PD的差是否为定值？如果是，请求出此定值；如果不是，请说明理由． （注：在解题过程中，如果你觉得有困难，可以阅读下面的材料）
    附阅读材料：
    ① 在平面直角坐标系中，若A、B两点的坐标分别为A（x1 ， y1），B（x2 ， y2），则A，B两点间的距离为|AB|= ，这个公式叫两点间距离公式．
    例如：已知A，B两点的坐标分别为（﹣1，2），（2，﹣2），则A，B两点间的距离为|AB|= =5．
    ② 因式分解：x4+2x2y2+y4=（x2+y2）2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个水池深3m,池中水深1m,现在要把水池中的水注满，每注水1h,池中的水深增加0.4m.

    （1）写出池中的水深y(m)与注水时间x(h)之间的函数关系式.

    （2）求自变量的取值范围.

    （3）画出这个函数的图像.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在下列解题过程的空白处填上适当的内容（推理的理由或数学表达式）

    如图，在△ABC中，已知∠ADE＝∠B，∠1＝∠2，FG⊥AB于点G.

    求证CD⊥AB.

    证明:∵∠ADE＝∠B（已知），

    ∴ （ ），

    ∵ DE∥BC（已证），

    ∴ （ ），

    又∵∠1＝∠2（已知），

    ∴ （ ），

    ∴CD∥FG（ ），

    ∴ （两直线平行同位角相等），

    ∵ FG⊥AB（已知），

    ∴∠FGB＝90°（垂直的定义）.

    即∠CDB＝∠FGB＝90°，

    ∴CD⊥AB. （垂直的定义）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【阅读材料】

    小明在学习二次根式时,发现一些含根号的式子可以化成另一式子的平方.如:

    5+2=(2+3)+2=()2+()2+2=()2;

    8+2=(3+5)+2=()2+()2+2=()2.

    【类比归纳】

    (1)请你仿照小明的方法将9+2化成一个式子的平方;

    (2)将下列等式补充完整:a+b+2=(　　　　)2(a≥0,b≥0),并证明这个等式;

    【变式探究】

    (3)若a+2=()2,且a,m,n均为正整数,则a=　　　　.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

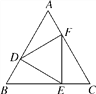
    【题目】如图，△ABC是等边三角形，点D，E，F分别是AB，BC，CA上的点．

    (1)若AD＝BE＝CF，问△DEF是等边三角形吗？试证明你的结论；

    (2)若△DEF是等边三角形，问AD＝BE＝CF成立吗？试证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列代数式：

    (1)； (2)ab÷c2； (3) ； (4) ； (5)2x(a+b)； (6)ab·2.

    符合代数式书写要求的有几个？答：（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B、C、D是四个城市，现在要建造一个火力发电厂M，为了节省资金，应使输电线路最短，因此电厂到这四个城市距离之和最小，请你确定M的位置.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料： 在数学课上，老师提出如下问题：
    小敏的作法如下：

    老师说：“小敏的作法正确．”依其作法，先得出ABCD，再得出矩形ABCD，请回答：以上两条结论的依据是 ．

    查看答案和解析>>

    同步练习册答案