
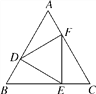
【题目】如图,△ABC是等边三角形,点D,E,F分别是AB,BC,CA上的点.
(1)若AD=BE=CF,问△DEF是等边三角形吗?试证明你的结论;
(2)若△DEF是等边三角形,问AD=BE=CF成立吗?试证明你的结论.
【答案】(1)△DEF是等边三角形,证明见解析;(2)AD=BE=CF成立,证明见解析.
【解析】试题分析:(1)由SAS易证△ADF≌△BED≌△CFE,所以DF=DE=EF,即△DEF是等边三角形;
(2)先证明∠1+∠2=120°,∠2+∠3=120°.可得∠1=∠3.同理∠3=∠4.则△ADF≌△BED≌△CFE,故能证明AD=BE=CF.
解:(1)△DEF是等边三角形.证明如下:
∵△ABC是等边三角形,
∴∠A=∠B=∠C,AB=BC=CA.
又∵AD=BE=CF,
∴DB=EC=FA.
∴△ADF≌△BED≌△CFE,
∴DF=ED=FE.∴△DEF是等边三角形.
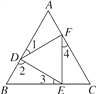
(2)AD=BE=CF成立.证明如下:如图,∵△DEF是等边三角形,∴DE=EF=FD,∠FDE=∠DEF=∠EFD=60°.∴∠1+∠2=120°.∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,∴∠2+∠3=120°,∴∠1=∠3.同理∠3=∠4,易证△ADF≌△BED≌△CFE(AAS),∴AD=BE=CF.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD垂直弦AC于点E,且交⊙O于点D,过点D作⊙O的切线与BA的延长线相交于点F,下列结论不一定正确的是( ) 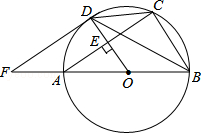
A.∠CDB=∠BFD
B.△BAC∽△OFD
C.DF∥AC
D.OD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是生活中常见的月历的示意图,请结合图示回答下列问题.
一 | 二 | 三 | 四 | 五 | 六 | 日 |
1 | 2 | 3 | 4 | 5 | ||
6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 | 14 | 15 | 16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 |
(1)如图是另一个月的月历,a表示该月中某一天,b,c,d是该月中其他3天,b,c,d分别与a的关系:b=________;c=________;d=________(用含a的代数式填空).
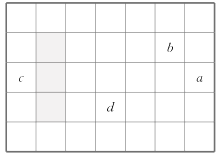
(2)用一个长方形框圈出月历中的三个数(如 图中的阴影),若这三个数之和等于51,则这三个数分别是多少?
(3)这样圈出的三个数的和可能是64吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图中方式用火柴棒搭正方形
![]()
①搭1个正方形需要 根火柴棒;
②搭2个正方形需要 根火柴棒,搭3个正方形需要 根火柴棒;
③搭10个这样的正方形需要多少根火柴棒;
④搭100个这样的正方形需要多少根火柴棒?
⑤如果用x表示所搭正方形的个数,那么搭x个这样的正方形需要多少根火柴棒?与同伴交流。
⑥根据你的计算方法,搭200个这样的正方形需要多少根火柴棒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?并说明理由;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,请按要求完成下列问题.
(1)用直尺和圆规作图,延长线段AB到点C,使BC=AB;反向延长线段AB到点D,使AD=AC;
(2)如果AB=2cm;①求CD的长度;②设点P是线段BD的中点,求线段CP的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
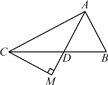
【题目】如图,在△ABC中,AD是∠BAC的平分线,且∠B=∠ADB,过点C作CM垂直于AD的延长线,垂足为M.
(1)若∠DCM=α,试用α表示∠BAD;
(2)求证:AB+AC=2AM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
(1)用含x的代数式表示地面总面积;
(2)当x=4,y=2时,铺1 m2地砖的平均费用为30元,那么铺地砖的总费用为多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com