
【题目】如图,在△ABC中,AD是∠BAC的平分线,且∠B=∠ADB,过点C作CM垂直于AD的延长线,垂足为M.
(1)若∠DCM=α,试用α表示∠BAD;
(2)求证:AB+AC=2AM.
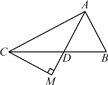
【答案】(1)∠BAD=2α;(2)证明见解析.
【解析】试题分析:(1)、根据垂直得出∠CDM=∠ADB=90°-α,然后根据∠BAD=180°-2∠ADB得出答案;(2)、延长AM到F使MF=AM,连结CF,根据AD为角平分线得出∠CAF=∠BAF=∠F,根据平行线的性质得出∠FCD=∠B=∠ADB=∠CDF,从而得出CF=DF,即AC=DF,从而得出答案.
试题解析:(1)、∵CM⊥AM,∠DCM=α,∴∠CDM=∠ADB=∠B=90°-α,
∴∠BAD=180°-2∠ADB=180°-2(90°-α)=2α.
(2)、证明:延长AM到F使MF=AM,连结CF,则有AC=CF,
∵AD平∠BAC,∴∠CAF=∠BAF=∠F,∴CF∥AB, ∴∠FCD=∠B=∠ADB=∠CDF,
∴CF=DF,∴AC=DF, ∵AD+DF=2AM,∴AB+AC=2AM.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是4, ![]() 的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则
的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则![]() 的最小值是( )
的最小值是( )

A. 2 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
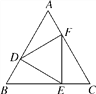
【题目】如图,△ABC是等边三角形,点D,E,F分别是AB,BC,CA上的点.
(1)若AD=BE=CF,问△DEF是等边三角形吗?试证明你的结论;
(2)若△DEF是等边三角形,问AD=BE=CF成立吗?试证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的平分线为OM,ON为∠MOA内的一条射线,OG为∠AOB外的一条射线.试说明:
(1)∠MON=![]() (∠BON-∠AON);
(∠BON-∠AON);
(2)∠MOG=![]() (∠AOG+∠BOG).
(∠AOG+∠BOG).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,直线![]() ,另一直线交
,另一直线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,且
,且![]() ,点
,点![]() 为直线
为直线![]() 上一动点,点
上一动点,点![]() 为直线
为直线![]() 上一动点,且
上一动点,且![]() .
.
(![]() )如图
)如图![]() ,当点
,当点![]() 在点
在点![]() 右边且点
右边且点![]() 在点
在点![]() 左边时,
左边时,![]() 的平分线交
的平分线交![]() 的平分线于点
的平分线于点![]() ,求
,求![]() 的度数;
的度数;
(![]() )如图
)如图![]() ,当点
,当点![]() 在点
在点![]() 右边且点
右边且点![]() 在点
在点![]() 右边时,
右边时,![]() 的平分线交
的平分线交![]() 的平分线于点
的平分线于点![]() ,求
,求![]() 的度数;
的度数;
(![]() )当点
)当点![]() 在点
在点![]() 左边且点
左边且点![]() 在点
在点![]() 左边时,
左边时,![]() 的平分线交
的平分线交![]() 的平分线所在直线交于点
的平分线所在直线交于点![]() ,请直接写出
,请直接写出![]() 的度数,不说明理由.
的度数,不说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(0,2),B(﹣2,0),点D是x轴上一个动点,以AD为一直角边在一侧作等腰直角三角形ADE,∠DAE=90°,若△ABD为等腰三角形时点E的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△DEC的一个顶点D在△ABC内部,且∠CAD+∠CBD=90°.
(1)如图1,若△ABC与△DEC均为等腰直角三角形,且∠ABC=∠DEC=90°,连接BE,求证:△ADC∽△BEC.
(2)如图2,若∠ABC=∠DEC=90°, ![]() =
= ![]() =n,BD=1,AD=2,CD=3,求n的值;
=n,BD=1,AD=2,CD=3,求n的值;
(3)如图3,若AB=BC,DE=EC,且∠ABC=∠DEC=135°,BD=a,AD=b,CD=c,请直接写出a、b、c三者满足的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为m. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com