
【题目】已知:△DEC的一个顶点D在△ABC内部,且∠CAD+∠CBD=90°.
(1)如图1,若△ABC与△DEC均为等腰直角三角形,且∠ABC=∠DEC=90°,连接BE,求证:△ADC∽△BEC.
(2)如图2,若∠ABC=∠DEC=90°, ![]() =
= ![]() =n,BD=1,AD=2,CD=3,求n的值;
=n,BD=1,AD=2,CD=3,求n的值;
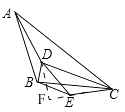
(3)如图3,若AB=BC,DE=EC,且∠ABC=∠DEC=135°,BD=a,AD=b,CD=c,请直接写出a、b、c三者满足的等量关系.
【答案】
(1)
证明: ∵△ABC与△DEC均为等腰直角三角形,且∠ABC=∠DEC=90°,
∴△ABC∽△DEC,
∴ ![]() ,∠ACB=∠DCE,
,∠ACB=∠DCE,
∴∠ACD=∠BCE,
∵ ![]() ,
,
∴△ACD∽△BCE
(2)
解:在Rt△ABC中,AC= ![]() =
= ![]() BC,
BC,
同理:CD= ![]() EC,
EC,
∵∠ABC=∠DEC=90°,
∵ ![]() =
= ![]() ,
,
∴ ![]()
∴△ABC∽△DEC,
∴ ![]() =
= ![]() ,∠ACB=∠DCE,
,∠ACB=∠DCE,
∴∠ACD=∠BCE,
∵ ![]() ,
,
∴△ACD∽△BCE,
∴ ![]() =
= ![]() ,
,
∴AD= ![]() BE,
BE,
∵AD=2,
∴BE= ![]() ,
,
在Rt△CDE中,CD2=DE2+CE2=(n2+1)CE2=9,
∴CE2= ![]()
∴DE2=n2CE2=n2× ![]() =
= ![]() ,
,
∵△ACD∽△BCE,
∴∠CAD=∠CBE,∵∠CAD+∠CBD=90°,
∴∠DBE=∠CBE+∠CBE=90°,
在Rt△BDE中,DE2=BD2+BE2=1+ ![]() ,
,
∴ ![]() =1+
=1+ ![]() ,
,
∴n=﹣ ![]() (舍)或n=
(舍)或n= ![]()
(3)
解:c2﹣b2=(2+ ![]() )a2,
)a2,
理由:如图,∵AB=BC,DE=EC,
∴ ![]() ,
,
∵∠ABC=∠DEC,
∴△ABC∽△DEC,
∴ ![]() ,
,
∵AB=BC,DE=EC,且∠ABC=∠DEC=135°,
∴∠ACB=∠DCE=22.5°,
∴∠ACD=∠BCE,
∵ ![]() ,
,
∴△ACD∽△BCE,
∴ ![]() ,
,
∴ ![]() ,
,
过点D作DF⊥CE交CE的延长线于F,
∵∠DEC=135°,
∴∠DEF=45°,
设DF=x,
∴EF=x,DE= ![]() x,
x,
∵EC=DE= ![]() x,
x,
∴CF=EF+EC=( ![]() +1)x,
+1)x,
在Rt△CDF中,CF2+DF2=CD2,
∴[( ![]() +1)x]2+x2=c2,
+1)x]2+x2=c2,
∴x2= ![]() ,
,
∴DE2=2x2= ![]() ,
,
∴BE2= ![]() =
= ![]() ×
× ![]() =
= ![]() ,
,
∵△ACD∽△BCE,
∴∠CAD=∠CBE,
∵∠CAD+∠CBD=90°,
∴∠DBE=∠CBE+∠CBE=90°,
在Rt△BDE中,DE2=BD2+BE2,
∴ ![]() =a2+
=a2+ ![]() ,
,
∴c2﹣b2=(2+ ![]() )a2.
)a2.
【解析】(1)先判断出△ABC∽△DEC,得出 ![]() ,即可得出结论;(2)先求出AC=
,即可得出结论;(2)先求出AC= ![]() BC,同理:CD=
BC,同理:CD= ![]() EC,再判断出△ABC∽△DEC,得出比例式,继而判断出△ACD∽△BCE,即可得出AD=
EC,再判断出△ABC∽△DEC,得出比例式,继而判断出△ACD∽△BCE,即可得出AD= ![]() BE,BE=
BE,BE= ![]() ,再利用勾股定理得出DE2=
,再利用勾股定理得出DE2= ![]() 再判断出∠DBE=90°,再用勾股定理得出DE的平方,用DE的平方建立方程求解即可;(3)同(2)的方法
再判断出∠DBE=90°,再用勾股定理得出DE的平方,用DE的平方建立方程求解即可;(3)同(2)的方法 ![]() ,再构造直角三角形,利用勾股定理即可得出结论.
,再构造直角三角形,利用勾股定理即可得出结论.


科目:初中数学 来源: 题型:
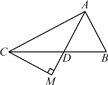
【题目】如图,在△ABC中,AD是∠BAC的平分线,且∠B=∠ADB,过点C作CM垂直于AD的延长线,垂足为M.
(1)若∠DCM=α,试用α表示∠BAD;
(2)求证:AB+AC=2AM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小力在电脑上设计了一个有理数运算程序:输入a,加※键,再输入b,得到运算a※b=a2-b2-[2(a-1)-![]() ]÷(a-b).
]÷(a-b).
(1)求(-2)※![]() 的值;
的值;
(2)小华在运用此程序计算时,屏幕显示“该程序无法操作”,你猜小华在输入数据时,可能出现什么情况?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为 ![]() π;小亮说此圆锥的弧长为
π;小亮说此圆锥的弧长为 ![]() π,则下列结论正确的是( )
π,则下列结论正确的是( ) 
A.只有小明对
B.只有小亮对
C.两人都对
D.两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
(1)用含x的代数式表示地面总面积;
(2)当x=4,y=2时,铺1 m2地砖的平均费用为30元,那么铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF 与AB、CD的延长线分别
交于E、F.
(1)证明:△BOE≌△DOF.
(2)当EF与AC满足什么条件时,四边形AECF是菱形,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON= ;∠CON= .
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=5°,求∠AOM.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com