[题目]如图.在△ABC中AD⊥BC.CE⊥AB.垂足分别为D.E.AD.CE交于点H.已知EH=EB=3.AE=4.则CH的长是( )A. 1 B. 2 C. 3 D. 4 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在△ABC中AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知EH=EB=3，AE=4，则CH的长是（）

A. 1 B. 2 C. 3 D. 4

【答案】D

【解析】试题分析：本题可先根据AAS判定△AEH≌△CEB，可得出AE=CE，从而得出CH=CE﹣EH=4﹣3=1．

解：在△ABC中，AD⊥BC，CE⊥AB，

∴∠AEH=∠ADB=90°；

∵∠EAH+∠AHE=90°，∠DHC+∠BCH=90°，

∵∠EHA=∠DHC（对顶角相等），

∴∠EAH=∠DCH（等量代换）；

∵在△BCE和△HAE中

，

∴△AEH≌△CEB（AAS）；

∴AE=CE；

∵EH=EB=3，AE=4，

∴CH=CE﹣EH=AE﹣EH=4﹣3=1．

故选A．

练习册系列答案

中考新航线系列答案

专项新评价中考二轮系列答案

中考研究全国各省市中考真题常考基础题系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图所示，某工程队准备在山坡（山坡视为直线l）上修一条路，需要测量山坡的坡度，即tanα的值．测量员在山坡P处（不计此人身高）观察对面山顶上的一座铁塔，测得塔尖C的仰角为31°，塔底B的仰角为26.6°．已知塔高BC=40米，塔所在的山高OB=240米，OA=300米，图中的点O、B、C、A、P在同一平面内．求：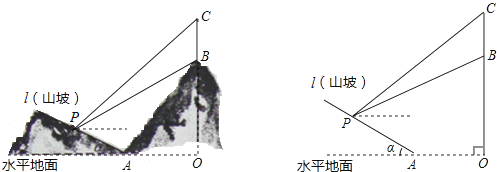

（1）P到OC的距离．
（2）山坡的坡度tanα．
（参考数据sin26.6°≈0.45，tan26.6°≈0.50；sin31°≈0.52，tan31°≈0.60）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，∠AOB的平分线为OM，ON为∠MOA内的一条射线，OG为∠AOB外的一条射线.试说明：

（1）∠MON=(∠BON-∠AON)；

（2）∠MOG=(∠AOG+∠BOG)．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：如图所示，直线，另一直线交于，交于，且，点为直线上一动点，点为直线上一动点，且．

（）如图，当点在点右边且点在点左边时，的平分线交的平分线于点，求的度数；

（）如图，当点在点右边且点在点右边时，的平分线交的平分线于点，求的度数；

（）当点在点左边且点在点左边时，的平分线交的平分线所在直线交于点，请直接写出的度数，不说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，点A（0，2），B（﹣2，0），点D是x轴上一个动点，以AD为一直角边在一侧作等腰直角三角形ADE，∠DAE=90°，若△ABD为等腰三角形时点E的坐标为．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】骑自相车旅行越来越受到人们的喜爱，顺风车行经营的A型车2016年4月份销售总额为3.2万元，今年经过改造升级后A型车每辆销售比去年增加400元，若今年4月份与去年4月份卖出的A型车数量相同，则今年4月份A型车销售总额将比去年4月份销售总额增加25%．
（1）求今年4月份A型车每辆销售价多少元（用列方程的方法解答）；
（2）该车行计划5月份新进一批A型车和B型车共50辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？ A、B两种型号车的进货和销售价格如表：

	A型车	B型车
进货价格（元/辆）	1100	1400
销售价格（元/辆）	今年的销售价格	2400

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：△DEC的一个顶点D在△ABC内部，且∠CAD+∠CBD=90°．
（1）如图1，若△ABC与△DEC均为等腰直角三角形，且∠ABC=∠DEC=90°，连接BE，求证：△ADC∽△BEC．

（2）如图2，若∠ABC=∠DEC=90°， = =n，BD=1，AD=2，CD=3，求n的值；

（3）如图3，若AB=BC，DE=EC，且∠ABC=∠DEC=135°，BD=a，AD=b，CD=c，请直接写出a、b、c三者满足的等量关系．