练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，∠AOB的平分线为OM，ON为∠MOA内的一条射线，OG为∠AOB外的一条射线.试说明：

    （1）∠MON=(∠BON-∠AON)；

    （2）∠MOG=(∠AOG+∠BOG)．

    【答案】（1）证明见解析；（2）证明见解析.

    【解析】根据角平分线定义和角的和差关系，得

    （1）∠BON－∠AON=∠BOM+∠MON－∠AON=(∠BOM－∠AON)+∠MON=∠MON+∠MON=2∠MON；

    （2）∠AOG+∠BOG=∠AOB+∠BOG+∠BOG=2∠MOB+2∠BOG=2(∠MOB+∠BOG)=2∠MOG.

    解：(1)因为，∠BON=∠BOM+∠MON，

    ∠BON－∠AON

    =∠BOM+∠MON－∠AON

    =(∠BOM－∠AON)+ ∠MON

    =∠MON+∠MON

    =2∠MON，

    所以，∠MON=(∠BON－∠AON)；

    (2)因为，∠AOG+∠BOG

    =∠AOB+∠BOG+∠BOG

    =2∠MOB+2∠BOG

    =2(∠MOB+∠BOG)

    =2∠MOG，

    所以，∠MOG=(∠AOG+∠BOG).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

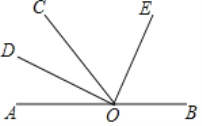
    【题目】如图所示，O为直线AB上一点，OD平分∠AOC，∠DOE=90°．

    （1）∠AOD的余角是 ______ ，∠COD的余角是 ______

    （2）OE是∠BOC的平分线吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，□ABCD中，点E、F在对角线AC上，且AE=CF。求证：四边形BEDF是平行四边形。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C在线段AB上，AC=8cm，CB=6cm，点M、N分别是AC、BC的中点．

    （1）求线段MN的长；

    （2）若C为线段AB上任一点，满足AC+CB=a cm，其它条件不变，你能猜想MN的长度吗？并说明理由；

    （3）若C在线段AB的延长线上，且满足AC﹣BC=b cm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？并说明理由；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知线段AB，请按要求完成下列问题．

    （1）用直尺和圆规作图，延长线段AB到点C，使BC=AB；反向延长线段AB到点D，使AD=AC；

    （2）如果AB=2cm；①求CD的长度；②设点P是线段BD的中点，求线段CP的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两个大小不同的等腰直角三角板如图①放置，图②是由它抽象出的几何图形，点B，C，E在同一条直线上，连接CD.求证：CD⊥BE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

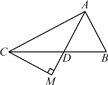
    【题目】如图，在△ABC中，AD是∠BAC的平分线，且∠B＝∠ADB，过点C作CM垂直于AD的延长线，垂足为M.

    (1)若∠DCM＝α，试用α表示∠BAD；

    (2)求证：AB＋AC＝2AM.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知EH=EB=3，AE=4，则CH的长是（ ）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF 与AB、CD的延长线分别

    交于E、F.

    (1)证明:△BOE≌△DOF.

    (2)当EF与AC满足什么条件时,四边形AECF是菱形,为什么?

    查看答案和解析>>

    同步练习册答案