
【题目】如图,在平面直角坐标系中,点A(0,2),B(﹣2,0),点D是x轴上一个动点,以AD为一直角边在一侧作等腰直角三角形ADE,∠DAE=90°,若△ABD为等腰三角形时点E的坐标为 . 
【答案】(2,2)或(2,4)或(2,2 ![]() )或(2,﹣2
)或(2,﹣2 ![]() )
)
【解析】解:连接EC. 
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△BAD和△ACE中, ,
,
∴△ABD≌△ACE,
∴BD=EC.∠ABD=∠ACE=45°,
∵∠ACB=45°,
∴∠ECD=90°,
∴点E在过点C垂直x轴的直线上,且EC=DB,①当DB=DA时,点D与O重合,BD=OB=2,此时E(2,2).②当AB=AD时,BD=CE=4,此时E(2,4).③当BD=AB=2 ![]() 时,E(2,2
时,E(2,2 ![]() )或(2,﹣2
)或(2,﹣2 ![]() ),
),
故答案为(2,2)或(2,4)或(2,2 ![]() )或(2,﹣2
)或(2,﹣2 ![]() ).
).
连接EC.只要证明△ABD≌△ACE,推出BD=EC.∠ABD=∠ACE=45°,由∠ACB=45°,推出∠ECD=90°,推出点E在过点C垂直x轴的直线上,且EC=DB,再分三种情形讨论即可解决问题.


科目:初中数学 来源: 题型:
【题目】如图是生活中常见的月历的示意图,请结合图示回答下列问题.
一 | 二 | 三 | 四 | 五 | 六 | 日 |
1 | 2 | 3 | 4 | 5 | ||
6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 | 14 | 15 | 16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 |
(1)如图是另一个月的月历,a表示该月中某一天,b,c,d是该月中其他3天,b,c,d分别与a的关系:b=________;c=________;d=________(用含a的代数式填空).
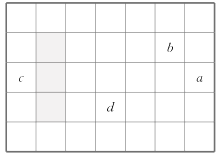
(2)用一个长方形框圈出月历中的三个数(如 图中的阴影),若这三个数之和等于51,则这三个数分别是多少?
(3)这样圈出的三个数的和可能是64吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,请按要求完成下列问题.
(1)用直尺和圆规作图,延长线段AB到点C,使BC=AB;反向延长线段AB到点D,使AD=AC;
(2)如果AB=2cm;①求CD的长度;②设点P是线段BD的中点,求线段CP的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
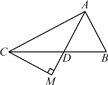
【题目】如图,在△ABC中,AD是∠BAC的平分线,且∠B=∠ADB,过点C作CM垂直于AD的延长线,垂足为M.
(1)若∠DCM=α,试用α表示∠BAD;
(2)求证:AB+AC=2AM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解并完成下面问题:
我们知道,任意一个正整数![]() 都可以进行这样的因式分解:
都可以进行这样的因式分解:![]() (
(![]() 是正整数),在
是正整数),在![]() 的所有这种分解中,如果
的所有这种分解中,如果![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是
是![]() 的最佳分解.并规定:
的最佳分解.并规定:
![]() (其中
(其中![]() ).例如:
).例如:![]() 可以分解成
可以分解成![]() ,
,![]() 或
或![]() ,因为
,因为![]() ,所以
,所以![]() 是
是![]() 的最佳分解,所以
的最佳分解,所以![]() .
.
(![]() )如果一个正整数
)如果一个正整数![]() 是另外一个正整数
是另外一个正整数![]() 的平方,我们称正整数
的平方,我们称正整数![]() 是完全平方数,若
是完全平方数,若![]() 是一个完全平方数,求
是一个完全平方数,求![]() 的值;
的值;
(![]() )如果一个两位正整数
)如果一个两位正整数![]() ,交换其个位数字与十位数字得到的新两位数减去原数所得的差为
,交换其个位数字与十位数字得到的新两位数减去原数所得的差为![]() ,那么我们称这个两位正整数
,那么我们称这个两位正整数![]() 为“吉祥数”,求符合条件的所有“吉祥数”;
为“吉祥数”,求符合条件的所有“吉祥数”;
(![]() )在(
)在(![]() )中的所有“吉祥数”中,求
)中的所有“吉祥数”中,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小力在电脑上设计了一个有理数运算程序:输入a,加※键,再输入b,得到运算a※b=a2-b2-[2(a-1)-![]() ]÷(a-b).
]÷(a-b).
(1)求(-2)※![]() 的值;
的值;
(2)小华在运用此程序计算时,屏幕显示“该程序无法操作”,你猜小华在输入数据时,可能出现什么情况?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
(1)用含x的代数式表示地面总面积;
(2)当x=4,y=2时,铺1 m2地砖的平均费用为30元,那么铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:我们知道|x|= ,
,
所以当x>0时,![]() =1; 当x<0时,
=1; 当x<0时,![]() =﹣1.现在我们可以用这个结论来解决下面问题:
=﹣1.现在我们可以用这个结论来解决下面问题:
(1)已知a,b是有理数,当ab≠0时,![]() =_____;
=_____;
(2)已知a,b,c是有理数,当abc≠0时,![]() =_____;
=_____;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,则![]() =_____.
=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com