
����Ŀ�����Ķ����ϡ�
С����ѧϰ���θ�ʽʱ,����һЩ�����ŵ�ʽ�ӿ��Ի�����һʽ�ӵ�ƽ��.��:
5+2![]() =(2+3)+2
=(2+3)+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() =(
=(![]() )2;
)2;
8+2![]() =(3+5)+2
=(3+5)+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() =(
=(![]() )2.
)2.
����ȹ��ɡ�
(1)�������С���ķ�����9+2![]() ����һ��ʽ�ӵ�ƽ��;
����һ��ʽ�ӵ�ƽ��;
(2)�����е�ʽ��������:a+b+2![]() =(��������)2(a��0,b��0),��֤�������ʽ;
=(��������)2(a��0,b��0),��֤�������ʽ;
����ʽ̽����
(3)��a+2![]() =(
=(![]() )2,��a,m,n��������,��a=��������.
)2,��a,m,n��������,��a=��������.
���𰸡�(1) (![]() )2;(2)����������3��11��13��17��31
)2;(2)����������3��11��13��17��31
�������������������1��������ȫƽ����ʽ�ɵã�
��2��������ȫƽ����ʽ��⣻
��3���ѵ�ʽ�ұ�չ�����ɵõ�m+n=a��mn=30�������������������õ�mn=1��30=15��2=5��6��10��3�����ǿɵ�m+n��ֵ��
���������
(1)9+2![]() =(7+2)+2
=(7+2)+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() =(
=(![]() )2.
)2.
(2) ![]() .
.
֤��:�ұ�=(![]() )2+2
)2+2![]() +(
+(![]() )2=a+b+2
)2=a+b+2![]() =���,
=���,
����a+b+2![]() =(
=(![]() )2.
)2.
(3)��a+2![]() =(
=(![]() )2��(
)2��(![]() )2��m+n+2
)2��m+n+2![]() ,
,
��m+n=a��mn=30,
�֡�30��1��30=15��2=5��6��10��3��
��m+n=31��17��11��13.


 ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��.ij����ʵʩ������ˮ�����ǰ���Ծ���������ˮ��������˵��飬�±���ͨ�������������õ�50����ͥȥ����ƽ����ˮ��![]() ��λ����
��λ����![]() �������������ݽ�������������
�������������ݽ�������������

Ƶ���ֲ���
���� | ���� | Ƶ�� |
| ���� | 11 |
|
| 19 |
| ||
�ϼ� |
| 2 50 |
![]() ������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
![]() ��ֱ��ͼ�����ܵõ�ʲô��Ϣ��
��ֱ��ͼ�����ܵõ�ʲô��Ϣ�� ![]() д����������
���������![]() ��
��
![]() Ϊ�˹�����Լ��ˮ��Ҫȷ��һ����ˮ���ı�������������IJ��ְ�
Ϊ�˹�����Լ��ˮ��Ҫȷ��һ����ˮ���ı�������������IJ��ְ�![]() ���۸��շѣ���Ҫʹ
���۸��շѣ���Ҫʹ![]() �ļ�ͥ�շѲ���Ӱ�죬����ü�ͥ�¾���ˮ��Ӧ�ö�Ϊ���٣�Ϊʲô��
�ļ�ͥ�շѲ���Ӱ�죬����ü�ͥ�¾���ˮ��Ӧ�ö�Ϊ���٣�Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����OΪֱ��AB��һ������O��������OC��ʹ��BOC=120������һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB������һ��ON��ֱ��AB���·���

��1����ͼ2����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ʹ��OM����BOC���ڲ�����OMǡ��ƽ����BOC����ʱ��AOM= �ȣ�
��2����ͼ3��������ͼ2�е����ǰ��Ƶ�O����ʱ�뷽����ת��ʹ��ON����AOC���ڲ�����̽����AOM����NOC֮������ʲô������ϵ����˵�����ɣ�
��3����ͼ1�е����ǰ��Ƶ�O��ÿ��10�����ٶ�����ʱ�뷽����תһ��������ת�Ĺ���������ֱ��ONǡ��ƽ����AOC�����ʱ���ǰ��Ƶ�O��ת��ʱ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ų�¼Ƭ��֮�¡��IJ�����ȫ���Կ�����Ⱦ����Խ��Խ���ӣ�����������������Ҳ��������������ӳ��ҹ�����A��B�����ͺŵĿ�������������֪һ̨A�Ϳ����������Ľ��۱�һ̨B�Ϳ����������Ľ��۶�300Ԫ����7500Ԫ����A�Ϳ�������������6000Ԫ����B�Ϳ�����������̨����ͬ��
��1����һ̨A�Ϳ�����������һ̨B�Ϳ����������Ľ��۸�Ϊ����Ԫ��
��2�������۹����У�A�Ϳ�����������Ϊ��������ǿ������С�����������ߵĻ�ӭ��Ϊ������B�Ϳ������������������������������B�Ϳ������������н������ۣ����г����飬��B�Ϳ������������ۼ�Ϊ1800Ԫʱ��ÿ�������4̨���ڴ˻����ϣ��ۼ�ÿ����50Ԫ��ÿ�콫���۳�1̨�����ÿ�������������B�Ϳ���������������Ϊ3200Ԫ�������������Ӧ��B�Ϳ������������ۼ۶�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���BAC=90�㣬AB=AC����DΪֱ��BC��һ���㣨��D����B��C�غϣ�����ADΪ����AD���Ҳ���������ADEF������CF��
��1���۲���룺��ͼ��1��������D���߶�BC��ʱ��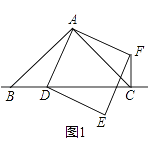
��BC��CF��λ�ù�ϵ�ǣ���
��BC��CD��CF֮���������ϵΪ����������ֱ��д�ں����ϣ�
��2����ѧ˼������ͼ��2��������D���߶�CB���ӳ�����ʱ�������١����еĽ����Ƿ���Ȼ�������������������֤������������������д����ȷ�����ٸ���֤����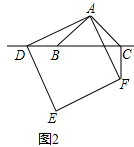
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�з�ʽ�û�����������
![]()
�ٴ�1����������Ҫ ��������
�ڴ�2����������Ҫ ����������3����������Ҫ ��������
�۴�10����������������Ҫ���ٸ�������
�ܴ�100����������������Ҫ���ٸ�������
�������x��ʾ���������εĸ�������ô��x����������������Ҫ���ٸ���������ͬ�齻����
������ļ��㷽������200����������������Ҫ���ٸ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016��11��13�հͻ�˹̹�ϴ������ʽ���ۣ��˸۳�Ϊ�ҹ���һ��һ·����չս���ϵ�һ���貵����ǣ�ij����Զ�����伯���������ͺŵ�Զ����֣�ÿ���ͺŵĻ�����������ӯ��������±���ʾ��
�� | �� | �� | |
ƽ���������صĶ�������֣� | 10 | 5 | 7.5 |
ƽ��ÿ�ֻ���ɻ����磨��Ԫ�� | 5 | 3.6 | 4 |
��1�������ҡ��������ͺŵĻ��ֹ�8�ң���55��ֵĻ������͵��ϴ���ۣ����ҡ��������ͺŵĻ��ָ������ң�
��2�����żƻ�δ���������ͺŵĻ��ֹ�20��װ��180��ֵĻ��ﵽ���ڣ������ҡ��������ͺŵĻ�������֮�Ͳ��������ͻ��ֵ��������������ͻ�����m�ң�����ͻ������ң����ͻ������ң��ú���m��ʽ�ӱ�ʾ������ô��ΰ���װ�ˣ���ʹ���Ż����������������Ķ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��2��0����B��0��2����������AOB��x���������������Ĺ������ڹ��������е�O�Ķ�Ӧ�����μ�Ϊ��O1 �� ��O2 �� ��O3������O10�������ǣ� ��
A.��16+4��0��
B.��14+4��2��
C.��14+3��2��
D.��12+3��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��1���������߾���A��1��0����C��0��3�����㣬��x�ύ�ڵ�B��
��1����ֱ��y=mx+n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
��2���������ߵĶԳ���x=��1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�������M�����ꣻ
��3�����PΪ�����ߵĶԳ���x=��1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com