
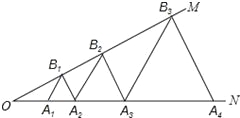
【题目】如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为 .
【答案】32
【解析】
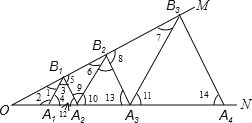
试题分析:根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2…进而得出答案.∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°, ∴∠2=120°,
∵∠MON=30°, ∴∠1=180°﹣120°﹣30°=30°, 又∵∠3=60°, ∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°, ∴OA1=A1B1=1, ∴A2B1=1, ∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°, ∵∠4=∠12=60°, ∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°, ∴A2B2=2B1A2,B3A3=2B2A3, ∴A3B3=4B1A2=4,
A4B4=8B1A2=8, A5B5=16B1A2=16, 以此类推:A6B6=32B1A2=32.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:把函数y=bx+a和函数y=ax+b(其中a,b是常数,且a≠0,b≠0)称为一对交换函数,其中一个函数是另一个函数的交换函数.比如,函数y=4x+1是函数y=x+4的交换函数,等等.
(1)直接写出函数y=2x+1的交换函数;_________________;并直接写出这对交换函数和x轴所围图形的面积为_____________________________;
(2)若一次函数y=ax+2a和其交换函数与x轴所围图形的面积为3,求a的值.
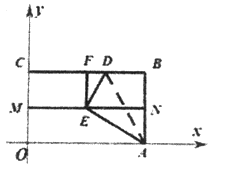
(3)如图,在平面直角坐标xOy中,矩形OABC中,点C(0, ![]() ),M、N分别是线段OC、AB的中点,将△ABD沿着折痕AD翻折,使点B的落点E恰好落在线段MN的中点,点F是线段BC的中点,连接EF,若一次函数
),M、N分别是线段OC、AB的中点,将△ABD沿着折痕AD翻折,使点B的落点E恰好落在线段MN的中点,点F是线段BC的中点,连接EF,若一次函数![]() 和
和![]() 与线段EF始终都有交点,则m的取值范围为_____________________.
与线段EF始终都有交点,则m的取值范围为_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量![]() 单位:吨
单位:吨![]() ,并将调查数据进行如下整理:
,并将调查数据进行如下整理:

频数分布表
分组 | 划记 | 频数 |
| 正正 | 11 |
|
| 19 |
| ||
合计 |
| 2 50 |
![]() 把上面频数分布表和频数分布直方图补充完整;
把上面频数分布表和频数分布直方图补充完整;
![]() 从直方图中你能得到什么信息?
从直方图中你能得到什么信息? ![]() 写出两条即可
写出两条即可![]() ;
;
![]() 为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按
为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按![]() 倍价格收费,若要使
倍价格收费,若要使![]() 的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为a的正方形上剪去一个边长为b的小正方形(a>b),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )

A. a2-b2=(a+b)(a-b) B. (a+b)2=a2+2ab+b2
C. (a-b)2=a2-2ab+b2 D. a2-ab=a(a-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】决心试一试,请阅读下列材料:计算:![]()
解法一:原式=![]()
=![]()
=![]()
解法二:原式=![]()
=![]()
=![]()
=![]()
解法三:原式的倒数为:![]()
=![]()
=﹣20+3﹣5+12
=﹣10
故原式 =![]()
上述得出的结果不同,肯定有错误的解法,你认为解法 是错误的,在正确的解法中,你认为解法 最简捷.然后请解答下列问题,计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
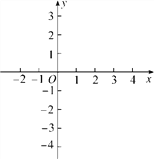
【题目】在下列平面直角坐标系中画出函数y1=-x+3,y2=3x-4的图象.观察图象,回答下列问题:
(1)当x取何值时,y1=y2?
(2)当x取何值时,y1>y2?
(3)当x取何值时,y1<y2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠AOM= 度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年11月13日巴基斯坦瓜达尔港正式开港,此港成为我国“一带一路”必展战略上的一颗璀璨的明星,某大型远洋运输集团有三种型号的远洋货轮,每种型号的货轮载重量和盈利情况如下表所示:
甲 | 乙 | 丙 | |
平均货轮载重的吨数(万吨) | 10 | 5 | 7.5 |
平均每吨货物可获例如(百元) | 5 | 3.6 | 4 |
(1)若用乙、丙两种型号的货轮共8艘,将55万吨的货物运送到瓜达尔港,问乙、丙两种型号的货轮各多少艘?
(2)集团计划未来用三种型号的货轮共20艘装运180万吨的货物到国内,并且乙、丙两种型号的货轮数量之和不超过甲型货轮的数量,如果设丙型货轮有m艘,则甲型货轮有艘,乙型货轮有艘(用含有m的式子表示),那么如何安排装运,可使集团获得最大利润?最大利润的多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com