
【题目】如图,在边长为a的正方形上剪去一个边长为b的小正方形(a>b),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )

A. a2-b2=(a+b)(a-b) B. (a+b)2=a2+2ab+b2
C. (a-b)2=a2-2ab+b2 D. a2-ab=a(a-b)
科目:初中数学 来源: 题型:
【题目】【背景】已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1,d2,d3,且d1=d3=1,d2=2.我们把四个顶点分别在l,m,n,k这四条平行线上的四边形称为“格线四边形” .
【探究1】(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线k于点F.求正方形ABCD的边长.
【探究2】(2)如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l,k于点G、点M.求证:EC=DF.
【拓展】(3)如图3,l∥k,等边△ABC的顶点A,B分别落在直线l,k上,AB⊥k于点B,且∠ACD=90°,直线CD分别交直线l、k于点G、点M,点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE,DH⊥l于点H.猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
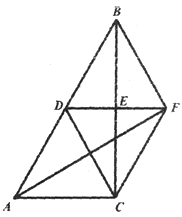
【题目】如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点D作DE⊥BC于E,过点C作AB的平行线与DE的延长线交于点F,连接BF,AF.
(1)求证:四边形BDCF为菱形:
(2)若四边形BDCF的面积为24,CE:AC=2:3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计![]() 两省人口总数基本相同,2001年A省的城镇在校中学生人数为156万,农村在校中学生人数为72万;B省的城镇在校中学生人数为84万,农村在校中学生人数为103万
两省人口总数基本相同,2001年A省的城镇在校中学生人数为156万,农村在校中学生人数为72万;B省的城镇在校中学生人数为84万,农村在校中学生人数为103万![]() 李军同学根据数据画出下面两个复合条形统计图.
李军同学根据数据画出下面两个复合条形统计图.

![]() 图______ 更好反映两省在校中学生总数;
图______ 更好反映两省在校中学生总数;
![]() 图______ 更好地比较
图______ 更好地比较![]() 省城镇和农村在校中学生人数;
省城镇和农村在校中学生人数;
![]() 说说两种图的特点.
说说两种图的特点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PAPC,连接CE,AE,OE,OE交CA于点D. 
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°,AP= ![]() AC,求证:DO=DP.
AC,求证:DO=DP.
查看答案和解析>>
科目:初中数学 来源: 题型:
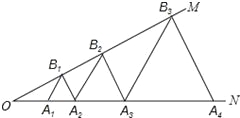
【题目】如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( ) 
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=﹣x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(﹣4,5),并与y轴交于点C,抛物线的对称轴为直线x=﹣1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=﹣1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com