
【题目】如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PAPC,连接CE,AE,OE,OE交CA于点D. 
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°,AP= ![]() AC,求证:DO=DP.
AC,求证:DO=DP.
【答案】
(1)解:∵PE2=PAPC,
∴ ![]() ,
,
∵∠APE=∠EPC,
∴△PAE∽△PEC
(2)解:如图1,
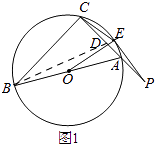
连接BE,
∴∠OBE=∠OEB,
∵∠OBE=∠PCE,
∴∠OEB=∠PCE,
∵△PAE∽△PEC,
∴∠PEA=∠PCE,
∴∠PEA=∠OEB,
∵AB为直径,
∴∠AEB=90°,
∴∠OEB+∠OEA=90°,
∵∠PEA+∠OEA=90°,
∴∠OEP=90°,
∵点E在⊙O上,
∴PE是⊙O的切线
(3)解:如图,
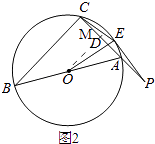
过点O作OM⊥AC于M,
∴AM= ![]() AC,
AC,
∵BC⊥AC,
∴OM∥BC,
∵∠ABC=30°,
∴∠AOM=30°,
∴OM= ![]() AM=
AM= ![]() AC,
AC,
∵AP= ![]() AC,
AC,
∴OM= ![]() AP,
AP,
∵PC=AC+AP=2AP+AP=3AP,
∴PE2=PA×PC=PA×3PA,
∴PE= ![]() PA,
PA,
∴OM=PE,
∵∠PED=∠OMD=90°,∠ODM=∠PDE,
∴△ODM≌△PDE,
∴OD=DP
【解析】(1)利用两边对应成比例,夹角相等,两三角形相似即可;(2)连接BE,转化出∠OEB=∠PCE,又由相似得出∠PEA=∠PCE,从而用直径所对的圆周角是直角,转化出∠OEP=90°即可;(3)构造全等三角形,先找出OD与PA的关系,再用等积式找出PE与PA的关系,从而判断出OM=PE,得出△ODM≌△PDE即可.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0),(m,0),且1<m<2,当x<﹣1时,y随x增大而减小,下列结论: ①abc>0;
②a+b<0;
③若点A(﹣3,y1),B(3,y2)在抛物线上,则y1<y2;
④a(m﹣1)+b=0;
⑤c≤﹣1时,则b2﹣4ac≤4a.
其中结论正确的有 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
尺规作图:作对角线等于已知线段的菱形.
已知:两条线段![]() 、
、![]() .
.

求作:菱形![]() ,使得其对角线分别等于
,使得其对角线分别等于![]() 和
和![]() .
.
小军的作法如下:
如图

(![]() )画一条线段
)画一条线段![]() 等于
等于![]() .
.
(![]() )分别以
)分别以![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的长为半径,在线段
的长为半径,在线段![]() 的上下各作两条弧,两弧相交于
的上下各作两条弧,两弧相交于![]() 、
、![]() 两点.
两点.
(![]() )作直线
)作直线![]() 交
交![]() 于
于![]() 点.
点.
(![]() )以
)以![]() 点为圆心,线段
点为圆心,线段![]() 的长为半径作两条弧,交直线
的长为半径作两条弧,交直线![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() 、
、![]() 、
、![]() .
.
所以四边形![]() 就是所求的菱形.
就是所求的菱形.
老师说:“小军的作法正确”.
该作图的依据是__________和___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H. 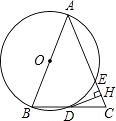
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:H为CE的中点;
(3)若BC=10,cosC= ![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为a的正方形上剪去一个边长为b的小正方形(a>b),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )

A. a2-b2=(a+b)(a-b) B. (a+b)2=a2+2ab+b2
C. (a-b)2=a2-2ab+b2 D. a2-ab=a(a-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只跳蚤在一数轴上从原点开始,第1次向右跳1个单位长度,紧接着第2次向左跳2个单位长度,第3次向右跳3个单位长度,第4次向左跳4个单位长度,…,依此规律跳下去,当它跳第100次落下时,所在位置表示的数是( )
A. 50 B. -50 C. 100 D. -100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OD平分∠AOC,∠DOE=90°,则以下结论正确的个数是( )
①∠AOD与∠BOE互为余角;②∠AOD=∠COE;③∠BOE=∠COE;④∠DOC与∠DOB互补.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】模型与应用.
(模型)
(1)如图①,已知AB∥CD,求证∠1+∠MEN+∠2=360°.

(应用)
(2)如图②,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6的度数为 .
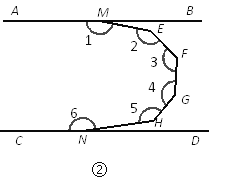
如图③,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为 .

(3)如图④,已知AB∥CD,∠AM1M2的角平分线M1 O与∠CMnMn-1的角平分线MnO交于点O,若∠M1OMn=m°.

在(2)的基础上,求∠2+∠3+∠4+∠5+∠6+……+∠n-1的度数.(用含m、n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com