
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H. 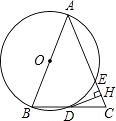
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:H为CE的中点;
(3)若BC=10,cosC= ![]() ,求AE的长.
,求AE的长.
【答案】
(1)解:DH与⊙O相切.理由如下:
连结OD、AD,如图,
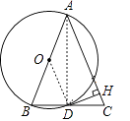
∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
而AO=BO,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DH⊥AC,
∴OD⊥DH,
∴DH为⊙O的切线
(2)证明:连结DE,如图,
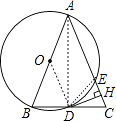
∵四边形ABDE为⊙O的内接四边形,
∴∠DEC=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠DEC=∠C,
∵DH⊥CE,
∴CH=EH,即H为CE的中点
(3)解:在Rt△ADC中,CD= ![]() BC=5,
BC=5,
∵cosC= ![]() =
= ![]() ,
,
∴AC=5 ![]() ,
,
在Rt△CDH中,∵cosC= ![]() =
= ![]() ,
,
∴CH= ![]() ,
,
∴CE=2CH=2 ![]() ,
,
∴AE=AC﹣CE=5 ![]() ﹣2
﹣2 ![]() =3
=3 ![]() .
.
【解析】(1)连结OD、AD,如图,先利用圆周角定理得到∠ADB=90°,则根据等腰三角形的性质得BD=CD,再证明OD为△ABC的中位线得到OD∥AC,加上DH⊥AC,所以OD⊥DH,然后根据切线的判定定理可判断DH为⊙O的切线;(2)连结DE,如图,有圆内接四边形的性质得∠DEC=∠B,再证明∠DEC=∠C,然后根据等腰三角形的性质得到CH=EH;(3)利用余弦的定义,在Rt△ADC中可计算出AC=5 ![]() ,在Rt△CDH中可计算出CH=
,在Rt△CDH中可计算出CH= ![]() ,则CE=2CH=2
,则CE=2CH=2 ![]() , 然后计算AC﹣CE即可得到AE的长.
, 然后计算AC﹣CE即可得到AE的长.


科目:初中数学 来源: 题型:
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为( ) 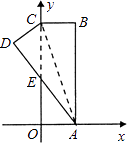
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,2),连接AB,点P是x轴上的一个动点,连接AP、BP,当△ABP的周长最小时,对应的点P的坐标和△ABP的最小周长分别为( )

A. (1,0), ![]() B. (3,0),
B. (3,0), ![]() C. (2,0),
C. (2,0), ![]() D. (2,0),
D. (2,0), ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径 ![]() 的长为( )
的长为( ) 
A.π
B.2π
C.4π
D.8π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整2h后提速行驶至乙地.设行驶时间为x( h),货车的路程为y1( km),小轿车的路程为y2( km ),图中的线段OA与折线OBCD分别表示y1,y2与x之间的函数关系.
(1)甲乙两地相距_____km,m=_____;
(2)求线段CD所在直线的函数表达式;
(3)小轿车停车休整后还要提速行驶多少小时,与货车之间相距20km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PAPC,连接CE,AE,OE,OE交CA于点D. 
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°,AP= ![]() AC,求证:DO=DP.
AC,求证:DO=DP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,∠AOE=∠DOF=90°,OP是∠BOC的平分线,∠AOD=40°.
(1)求∠EOP的度数;
(2)写出∠AOD的补角和余角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com