
����Ŀ��ģ����Ӧ��.
��ģ�ͣ�
��1����ͼ������֪AB��CD����֤��1����MEN����2��360��.

��Ӧ�ã�
��2����ͼ�ڣ���֪AB��CD�����1+��2+��3+��4+��5+��6�Ķ���Ϊ ��
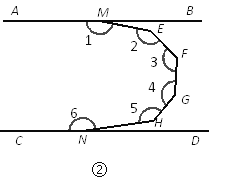
��ͼ�ۣ���֪AB��CD�����1+��2+��3+��4+��5+��6��������n�Ķ���Ϊ ��

��3����ͼ�ܣ���֪AB��CD����AM1M2�Ľ�ƽ����M1 O���CMnMn��1�Ľ�ƽ����MnO���ڵ�O������M1OMn��m�㣮

�ڣ�2���Ļ����ϣ����2+��3+��4+��5+��6����������n��1�Ķ��������ú�m��n�Ĵ���ʽ��ʾ��
���𰸡���1��֤������������2��900�� ��180��(n��1)����3��(180n��180��2m)��
����������1������E��EF��CD������ƽ����ͬһֱ�ߵ�����ֱ����ƽ�пɵ�EF��AB��������ֱ��ƽ�У�ͬ���ڽǻ����ɵá�1����MEF��180�㣬��2����NEF��180�������ɵá�1����2����MEN��360�� ����2�����ֱ��E�㣬F�㣬G�㣬H����L1��L2��L3��L4ƽ����AB�����ã�1���ķ����ɵá�1+��2+��3+��4+��5+��6=180��5=900������������Ľ��ⷽ���ɵô𰸣���3������O��SR��AB������ƽ����ͬһֱ�ߵ�����ֱ����ƽ�пɵ�SR��CD��������ֱ��ƽ�У��ڴ�����ȿɵá�AM1O����M1OR����C MnO����MnOR�����ԡ�A M1O����CMnO����M1OR����MnOR�����ɵá�A M1O����CMnO����M1OMn��m�㣬���ݽ�ƽ���ߵĶ���ɵá�AM1M2��2��A M1O����CMnMn-1��2��CMnO���ɴ˿ɵá�AM1M2����CMnMn-1��2��AM1O��2��CMnO��2��M1OMn��2m�㣬�����A M1E����2+��3+��4+��5+��6����������n��1����CMnMn-1��180��(n��1)���ɴ˿ɵ�
��2+��3+��4+��5+��6��������n��1��(180n��180��2m)��.
��ģ�͡�
��1����ͼ������֪AB��CD����֤��1����2����MEN��360��.
֤��������E��EF��CD��
��AB��CD��
��EF��AB��
���1����MEF��180�㣬
ͬ����2����NEF��180��
���1����2����MEN��360��
��Ӧ�á�
��2��900�� �� 180��(n��1)
�ֱ��E�㣬F�㣬G�㣬H����L1��L2��L3��L4ƽ����AB�����ã�1���ķ����ɵá�1+��2+��3+��4+��5+��6=180��5=900�㣻
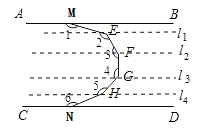
������Ľ��ⷽ���ɵã���1+��2+��3+��4+��5+��6��������n=180��(n��1)��
��3������O��SR��AB��
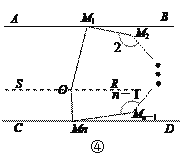
��AB��CD��
��SR��CD��
���AM1O����M1OR
ͬ����C MnO����MnOR
���A M1O����CMnO����M1OR����MnOR��
���A M1O����CMnO����M1OMn��m�㣬
��M1Oƽ�֡�AM1M2��
���AM1M2��2��A M1O��
ͬ����CMnMn-1��2��CMnO��
���AM1M2����CMnMn-1��2��AM1O��2��CMnO��2��M1OMn��2m�㣬
�֡ߡ�A M1E����2+��3+��4+��5+��6����������n��1����CMnMn-1��180��(n��1)��
���2+��3+��4+��5+��6��������n��1��(180n��180��2m)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��ABC���Բ��O��ֱ������P���߶�CA�ӳ�����һ�㣬��E��Բ��������PE2=PAPC������CE��AE��OE��OE��CA�ڵ�D�� 
��1����֤����PAE�ס�PEC��
��2����֤��PEΪ��O�����ߣ�
��3������B=30�㣬AP= ![]() AC����֤��DO=DP��
AC����֤��DO=DP��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�����ڵĻ���·�DZ߳�Ϊ1000��������ABCD.����1�š�2�������������ֱ�ӳ���A�;���Cͬʱ������1�ų�˳ʱ�롢2�ų���ʱ���ػ���·����ѭ����ʻ�����ο���ʱ��ѳ˳�(�ϡ��³���ʱ����Բ���)�������ٶȾ�Ϊ200��/��������ʻʱ��Ϊt��������������⣺
(1)��0��t��10ʱ���ֱ�д��1�ų���2�ų�����뻷�������A��·��(�ú�t�Ĵ���ʽ��ʾ)��
(2)��0��t��10ʱ������������·����400��ʱ��tֵ��
(3)��tΪ��ֵʱ��1�ų�������ǡ�þ�������C����ֱ��д����һ��ʱ��������2�ų������Ĵ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ش��������⣺
(1)�Ƚϡ�FOD���FOE�Ĵ�С��
(2)�������ǰ�Ƚϡ�DOE���BOF�Ĵ�С��
(3)�����������Ƚϡ�AOE���DOF�Ĵ�С��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�

��1����ͼ1���ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮��֤���е��ı���EFGH��ƽ���ı��Σ�
��2����ͼ2����P���ı���ABCD��һ�㣬������PA=PB��PC=PD����APB=��CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��3�����ı䣨2���е�������ʹ��APB=��CPD=90�㣬�����������䣬ֱ��д���е��ı���EFGH����״��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��y=��x+1��������y=ax2+bx+c��a��0���ཻ�ڵ�A��1��0���͵�D����4��5��������y�ύ�ڵ�C�������ߵĶԳ���Ϊֱ��x=��1������������x�ύ����һ��B��
��1����������ߵĺ�������ʽ��
��2������E��ֱ���·��������ϵ�һ�����㣬�����ACE��������ֵ��
��3����ͼ2������M��ֱ��x=��1��һ�㣬��N���������ϣ��Ե�A��D��M��NΪ������ı����ܷ��Ϊƽ���ı��Σ����ܣ���ֱ��д����M�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC��DΪBC�ߵ��е㣬����D��DE��AB��DF��AC������ֱ�ΪE��F.
(1)��֤����BED�ա�CFD��
(2)����A��60����BE��1������ABC���ܳ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�����ݣ�10��17��15��10��18��20������˵��������ǣ� ��
A.�����16
B.������ ![]()
C.������10
D.ƽ������15
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com