【题目】如图，某景区内的环形路是边长为1000米的正方形ABCD.现有1号、2号两辆游览车分别从出口A和景点C同时出发，1号车顺时针、2号车逆时针沿环形路连续循环行驶，供游客随时免费乘车(上、下车的时间忽略不计)，两车速度均为200米/分，设行驶时间为t分，解决下列问题：
(1)当0≤t≤10时，分别写出1号车、2号车在左半环线离出口A的路程(用含t的代数式表示)；
(2)当0≤t≤10时，求当两车相距的路程是400米时的t值；
(3)当t为何值时，1号车第三次恰好经过景点C？并直接写出这一段时间内它与2号车相遇的次数．
【答案】(1) 200t米， (2000－200t)米；(2) t的值为4或6；(3)这一段时间内它与2号车相遇的次数为5次．
【解析】（1）根据路程＝速度×时间结合AB、BC的长度，即可得出结论；
（2）分相遇前和相遇后两种情况找出关于t的一元一次方程，解之即可得出结论；
（3）1号车第三次恰好经过景点C行驶的路程，再由时间＝路程÷速度即可求得t的值．
(1)1号车在左半环线离出口A的路程为200t米，2号车在左半环线离出口A的路程为(2000－200t)米；
(2)当相遇前相距400米时，可列方程2000－200t－200t＝400，解得t＝4；
当相遇后相距400米时，可列方程200t＋200t－2000＝400，解得t＝6.
答：当两车相距的路程是400米时，t的值为4或6.
(3)由题意，得1号车第三次恰好经过景点C行驶的路程为1000×2＋1000×4×2＝10000(米)，所以1号车第三次恰好经过景点C需要的时间为t＝10000÷200＝50(分)；
这一段时间内它与2号车相遇的次数为5次．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】在数学课上，老师提出如下问题：
尺规作图：作对角线等于已知线段的菱形．
已知：两条线段
、
．
求作：菱形
，使得其对角线分别等于和
．
小军的作法如下：
如图
（
）画一条线段
等于．
（
）分别以
、
为圆心，大于
的长为半径，在线段的上下各作两条弧，两弧相交于
、
两点．
（
）作直线
交于
点．
（
）以点为圆心，线段的长为半径作两条弧，交直线于
、
两点，连接
、
、
、
．
所以四边形就是所求的菱形．
老师说：“小军的作法正确”．
该作图的依据是__________和___________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一只跳蚤在一数轴上从原点开始，第1次向右跳1个单位长度，紧接着第2次向左跳2个单位长度，第3次向右跳3个单位长度，第4次向左跳4个单位长度，…，依此规律跳下去，当它跳第100次落下时，所在位置表示的数是( )
A. 50 B. －50 C. 100 D. －100
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，O是直线AB上一点，OD平分∠AOC，∠DOE＝90°，则以下结论正确的个数是( )
①∠AOD与∠BOE互为余角；②∠AOD＝∠COE；③∠BOE＝∠COE；④∠DOC与∠DOB互补．
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明在学习了数据的收集、整理与描述后，为妈妈整理记录了10月份的家庭支出情况，并绘制成如下尚不完整的统计图表，请你根据图表信息完成下列各题：
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | 400 |
（1）10月份小明家共支出多少元？
（2）在扇形统计图中，表示“其他费”的扇形圆心角为多少度？
（3）请将表格补充完整；
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | 400 |
（4）请将条形统计图补充完整．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】模型与应用.
（模型）
（1）如图①，已知AB∥CD，求证∠1＋∠MEN＋∠2＝360°.
（应用）
（2）如图②，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6的度数为 ．
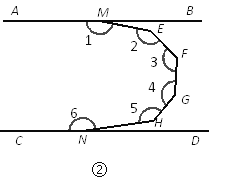
如图③，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6＋…＋∠n的度数为 ．
（3）如图④，已知AB∥CD，∠AM1M2的角平分线M1 O与∠CMnMn－1的角平分线MnO交于点O，若∠M1OMn＝m°．
在（2）的基础上，求∠2+∠3+∠4+∠5+∠6＋……＋∠n－1的度数．（用含m、n的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
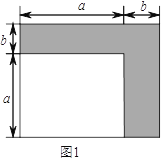
【题目】数学课上，我们知道可以用图形的面积来解释一些代数恒等式，如图
可以解释完全平方公式：
．
（）如图
（图中各小长方形大小均相等），请用两种不同的方法求图中阴影部分的面积（不化简）：
方法：______________________．
方法：______________________．
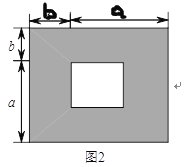
（）由（）中两种不同的方法，你能得到怎样的等式？请说明这个等式成立；
（
）已知
，
，请利用（）中的等式，求
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
