
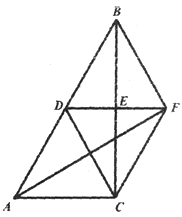
【题目】如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点D作DE⊥BC于E,过点C作AB的平行线与DE的延长线交于点F,连接BF,AF.
(1)求证:四边形BDCF为菱形:
(2)若四边形BDCF的面积为24,CE:AC=2:3,求AF的长.
【答案】(1) 见解析;(2) ![]()
【解析】(1)求出四边形ADFC是平行四边形,推出CF=AD=BD,根据平行四边形的判定得出四边形BDCF是平行四边形,再证CD=BD即可;
(2)设CE=2x,AC=3x,求出BC=4x,DF=AC=3x,根据菱形的面积公式求出x,再根据勾股定理求出AF即可.
解:(1)证明:DE⊥BC,∠ACB=90°,
∴∠BED=∠ACB,
∴DF∥AC,
∵CF∥AB,
∴四边形ADFC是平行四边形,
∴AD=CF,
∵D为AB的中点,
∴AD=BD,
∴BD=CF,
∵BD∥CF,
∴四边形BDCF是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴DC=BD,
∴四边形BDCF是菱形;
(2)∵CE:AC=2:3,
∴设CE=2x,AC=3x,
∵四边形BDCF是菱形,
∴BE=CE=2x,
∴BC=4x,
∵四边形ADFC是平行四边形,
∴DF=AC=3x,
∵四边形BDCF的面积为24,
∴![]() ×BC×DF=24,
×BC×DF=24,
∴![]() 4x3x=24,
4x3x=24,
解得:x=![]() 2(负数舍去),
2(负数舍去),
∴CE=4,DF=6,
∴AC=6,EF=![]() DF=3
DF=3
作FG⊥AC交AC的延长线于点G,可得矩形ECGF,
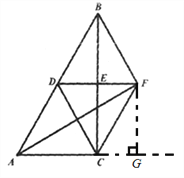
∴FG=CE=4,AG=AC+CG=6+3=9,
在Rt△AFG中,
由勾股定理得,AF=![]() .
.


科目:初中数学 来源: 题型:
【题目】为节约用电,某市根据每户居民每月用电量分为三档收费.第一档电价:每月用电量低于240度,每度0.4883元;第二档电价:每月用电量为240~400度,每度0.5383元;第三档电价:每月用电量为不低于400度,每度0.7883元.小灿同学对该市有1000户居民的某小区居民月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是( )

A. 本次抽样调查的样本容量为50 B. 估计该小区按第一档电价交费的居民户数最多
C. 该小区按第二档电价交费的居民有220户 D. 该小区按第三档电价交费的居民比例约为6%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知△ABC是等腰三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
(1)试猜想线段BG和AE的数量关系;
(2)如图②,将正方形DEFG绕点D按逆时针方向旋转α(0°<α≤90°),判断(1)中的结论是否仍然成立,证明你的结论.

(3)若BC=DE=2,在(2)的旋转过程中,求线段AE长的最大值和最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
尺规作图:作对角线等于已知线段的菱形.
已知:两条线段![]() 、
、![]() .
.

求作:菱形![]() ,使得其对角线分别等于
,使得其对角线分别等于![]() 和
和![]() .
.
小军的作法如下:
如图

(![]() )画一条线段
)画一条线段![]() 等于
等于![]() .
.
(![]() )分别以
)分别以![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的长为半径,在线段
的长为半径,在线段![]() 的上下各作两条弧,两弧相交于
的上下各作两条弧,两弧相交于![]() 、
、![]() 两点.
两点.
(![]() )作直线
)作直线![]() 交
交![]() 于
于![]() 点.
点.
(![]() )以
)以![]() 点为圆心,线段
点为圆心,线段![]() 的长为半径作两条弧,交直线
的长为半径作两条弧,交直线![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() 、
、![]() 、
、![]() .
.
所以四边形![]() 就是所求的菱形.
就是所求的菱形.
老师说:“小军的作法正确”.
该作图的依据是__________和___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:把函数y=bx+a和函数y=ax+b(其中a,b是常数,且a≠0,b≠0)称为一对交换函数,其中一个函数是另一个函数的交换函数.比如,函数y=4x+1是函数y=x+4的交换函数,等等.
(1)直接写出函数y=2x+1的交换函数;_________________;并直接写出这对交换函数和x轴所围图形的面积为_____________________________;
(2)若一次函数y=ax+2a和其交换函数与x轴所围图形的面积为3,求a的值.
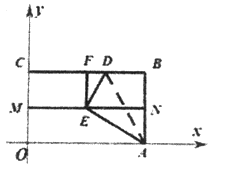
(3)如图,在平面直角坐标xOy中,矩形OABC中,点C(0, ![]() ),M、N分别是线段OC、AB的中点,将△ABD沿着折痕AD翻折,使点B的落点E恰好落在线段MN的中点,点F是线段BC的中点,连接EF,若一次函数
),M、N分别是线段OC、AB的中点,将△ABD沿着折痕AD翻折,使点B的落点E恰好落在线段MN的中点,点F是线段BC的中点,连接EF,若一次函数![]() 和
和![]() 与线段EF始终都有交点,则m的取值范围为_____________________.
与线段EF始终都有交点,则m的取值范围为_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为a的正方形上剪去一个边长为b的小正方形(a>b),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )

A. a2-b2=(a+b)(a-b) B. (a+b)2=a2+2ab+b2
C. (a-b)2=a2-2ab+b2 D. a2-ab=a(a-b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com