
【题目】为节约用电,某市根据每户居民每月用电量分为三档收费.第一档电价:每月用电量低于240度,每度0.4883元;第二档电价:每月用电量为240~400度,每度0.5383元;第三档电价:每月用电量为不低于400度,每度0.7883元.小灿同学对该市有1000户居民的某小区居民月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是( )

A. 本次抽样调查的样本容量为50 B. 估计该小区按第一档电价交费的居民户数最多
C. 该小区按第二档电价交费的居民有220户 D. 该小区按第三档电价交费的居民比例约为6%
【答案】C
【解析】A、根据样本容量的计算方法求解即可;B、C、D用样本去估计总体即可求解.
A、本次抽样调查的样本容量为:4+12+14+11+6+3=50,故选项A说法合理,不符合题意;
B、在样本中,按第一档电价交费的比例为:![]() ,该小区按第一档电价交费的居民户数为:1000×60%=600户;按第二档电价交费的比例为:
,该小区按第一档电价交费的居民户数为:1000×60%=600户;按第二档电价交费的比例为:![]() ,该小区按第一档电价交费的居民户数为:1000×34%=340户;按第三档电价交费的比例为:
,该小区按第一档电价交费的居民户数为:1000×34%=340户;按第三档电价交费的比例为:![]() ,该小区按第一档电价交费的居民户数为:1000×6%=60户. 故选项A说法合理,不符合题意;
,该小区按第一档电价交费的居民户数为:1000×6%=60户. 故选项A说法合理,不符合题意;
C、由选项B知该小区按第二档电价交费的比例为:![]() ,该小区按第一档电价交费的居民户数为:1000×34%=340户,故该选项说法不合理;
,该小区按第一档电价交费的居民户数为:1000×34%=340户,故该选项说法不合理;
D、该小区按第三档电价交费的居民比例约为6%,该说法合理,不符合题意.
故选C.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是( )
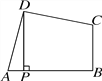
A. 3 B. 2![]() C. 3
C. 3![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【背景】已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1,d2,d3,且d1=d3=1,d2=2.我们把四个顶点分别在l,m,n,k这四条平行线上的四边形称为“格线四边形” .
【探究1】(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线k于点F.求正方形ABCD的边长.
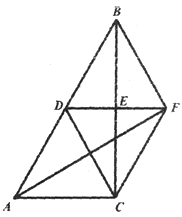
【探究2】(2)如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l,k于点G、点M.求证:EC=DF.
【拓展】(3)如图3,l∥k,等边△ABC的顶点A,B分别落在直线l,k上,AB⊥k于点B,且∠ACD=90°,直线CD分别交直线l、k于点G、点M,点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE,DH⊥l于点H.猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s. 
(1)求PQ的长;
(2)当直线AB与⊙O相切时,求证:AB⊥PN;
(3)当t为何值时,直线AB与⊙O相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
近五年,我国对外贸易发展迅速.据海关统计,2017年我国进出口总额为27.8万亿元,比2016年增长14.4%,其中2017年进口额12.5万亿元,比2016年增长19.0%.2013---2016年我国进出口额数据如下表:
年份 | 2013 | 2014 | 2015 | 2016 |
出口额/万亿元 | 13.7 | 14.4 | 14.1 | 13.8 |
进口额/万亿元 | 12.1 | 12.0 | 10.4 | 10.5 |
根据以上材料解答下列问题:
(1)2017年我国出口额为______________万亿元;
(2)请选择适当的统计图描述2013---2017年我国出口额,并在图中标明相应数据;
(3)通过(2)中的统计图判断:2013---2017年我国出口额比上一年增长最多的是_______________年.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在格线上.线段AB的两个端点也在格点上.
(1)若将线段AB绕点O逆时针旋转90°得到线段A1B1,试在图中画出线段A1B1.
(2)若线段A2B2与线段A1B1关于y轴对称,请画出线段A2B2.
(3)若点P是此平面直角坐标系内的一点,当点A、B1、B2、P四边围成的四边形为平行四边形时,请你直接写出点P的坐标(写出一个即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点D作DE⊥BC于E,过点C作AB的平行线与DE的延长线交于点F,连接BF,AF.
(1)求证:四边形BDCF为菱形:
(2)若四边形BDCF的面积为24,CE:AC=2:3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com