练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】据统计两省人口总数基本相同，2001年A省的城镇在校中学生人数为156万，农村在校中学生人数为72万；B省的城镇在校中学生人数为84万，农村在校中学生人数为103万李军同学根据数据画出下面两个复合条形统计图．

    图______ 更好反映两省在校中学生总数；

    图______ 更好地比较省城镇和农村在校中学生人数；

    说说两种图的特点．

    【答案】（1） （2） (3)答案详见解析.

    【解析】试题分析：（1）（2）根据两个图直接可以写出答案；

    （3）根据（1）、（2）比较的结果写出即可．

    试题解析：

    解：（1）图（2）更好反映两省在校中学生总数；

    故答案为：（2）；

    （2）图（1）更好地比较A（B）省城镇和农村在校中学生人数；

    故答案为：（1）；

    （3）图（1）更直观地反映本省城镇与农村在校中学生人数的差别；

    图（2）更好反映两省在校中学生总数的差别．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】(1)如果－axym是关于x，y的单项式，且系数是4，次数是5，那么a与m的值分别是________；

    (2)如果－(a－2)xym是关于x，y的五次单项式，那么a与m应满足的条件是____________；

    (3)如果单项式2x3y4与－x2zn的次数相同，那么n＝________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，已知△ABC是等腰三角形，∠BAC=90°，点D是BC的中点，作正方形DEFG，使点A、C分别在DG和DE上，连接AE、BG．

    （1）试猜想线段BG和AE的数量关系；

    （2）如图②，将正方形DEFG绕点D按逆时针方向旋转α（0°＜α≤90°），判断（1）中的结论是否仍然成立，证明你的结论．

    (3)若BC=DE=2,在（2）的旋转过程中,求线段AE长的最大值和最小值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：把函数y=bx+a和函数y=ax+b（其中a，b是常数，且a≠0，b≠0）称为一对交换函数，其中一个函数是另一个函数的交换函数．比如，函数y=4x+1是函数y=x+4的交换函数，等等．

    (1)直接写出函数y=2x+1的交换函数；_________________；并直接写出这对交换函数和x轴所围图形的面积为_____________________________；

    (2)若一次函数y=ax+2a和其交换函数与x轴所围图形的面积为3，求a的值．

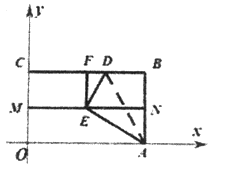
    (3)如图，在平面直角坐标xOy中，矩形OABC中，点C(0， )，M、N分别是线段OC、AB的中点，将△ABD沿着折痕AD翻折，使点B的落点E恰好落在线段MN的中点，点F是线段BC的中点，连接EF，若一次函数和与线段EF始终都有交点，则m的取值范围为_____________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算下面各题.
    （1）计算： +（1﹣ ）0﹣4cos45°．
    （2）解方程组： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】.某区在实施居民用水额定管理前，对居民生活用水情况进行了调查，下表是通过简单随机抽样获得的50个家庭去年月平均用水量单位：吨，并将调查数据进行如下整理：

    频数分布表

    分组

    划记

    频数

    正正

    11

    19

    合计

    2

    50

    把上面频数分布表和频数分布直方图补充完整；

    从直方图中你能得到什么信息？ 写出两条即可；

    为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按倍价格收费，若要使的家庭收费不受影响，你觉得家庭月均用水量应该定为多少？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为a的正方形上剪去一个边长为b的小正方形(a＞b)，把剩下的部分剪拼成一个梯形，分别计算这两个图形阴影部分的面积，由此可以验证的等式是(　)

    A. a2－b2＝(a＋b)(a－b) B. (a＋b)2＝a2＋2ab＋b2

    C. (a－b)2＝a2－2ab＋b2 D. a2－ab＝a(a－b)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

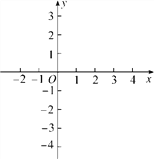
    【题目】在下列平面直角坐标系中画出函数y1＝－x＋3，y2＝3x－4的图象．观察图象，回答下列问题：

    (1)当x取何值时，y1＝y2?

    (2)当x取何值时，y1＞y2?

    (3)当x取何值时，y1＜y2?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合），以AD为边在AD的右侧作正方形ADEF，连接CF．
    （1）观察猜想：如图（1），当点D在线段BC上时，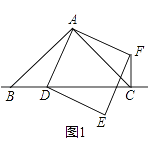

    ①BC与CF的位置关系是：；
    ②BC、CD、CF之间的数量关系为：（将结论直接写在横线上）
    （2）数学思考：如图（2），当点D在线段CB的延长线上时，上述①、②中的结论是否仍然成立？若成立，请给予证明，若不成立，请你写出正确结论再给予证明．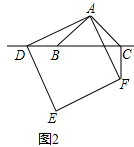

    查看答案和解析>>

    同步练习册答案