
【题目】2019年10月18日至27日(共10天)武汉军运会期间,从19日起武汉体育中心9天中接收观众人数的变化情况如下表(正数表示比前一天多的人数,负数表示经前一天少的人数):
日期 | 19日 | 20日 | 21日 | 2日 | 23日 | 24日 | 25日 | 26日 | 27日 |
人数变化/万人 | +0.5 | +0.7 | +0.8 | -0.4 | -0.6 | +0.2 | +0.3 | +0.5 | +0.2 |
(1)请判断这9天中,游客人数最多和最少的各是哪一天?它们相差多少万人?
(2)如果10月18日观众人数为2万人,平均每人门票100元,请问武汉体育中心在军运会这10天期间门票总收入为多少万元?
【答案】(1)10月27日人数最多,10月19日人数最少;相差1.2万人;(2)3320万元
【解析】
(1)由表格可知10月27日人数最多,10月23日人数最少,设18日有x万人,用x分别表示出27日和23日的人数再进行计算;
(2)依次求出10月19日至27日的观众人数,再列式计算即可.
(1)10月27日人数最多,10月23日人数最少
设18日有x万人,
则27日人数为![]()
=![]() (万人)
(万人)
23日人数为![]()
=![]() (万人)
(万人)
(![]() )-(
)-(![]() )=1.2万人
)=1.2万人
(2)∵10月18日观众人数为2万人,
∴10月19日至27日的观众人数依次是:2.5、3.2、4、3.6、3、3.2、3.5、4、4.2万人,
∴这10天期间门票总收入为:
![]() (万元)
(万元)


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
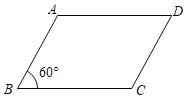
【题目】过某矩形的两个相对的顶点作平行线,再沿着平行线剪下两个直角三角形,剩余的图形为如图所示的ABCD,AB=4,BC=6,∠ABC=60°,则原来矩形的面积是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有3本和6本数学课本整齐地叠放在讲台上,请根据图中所给的数据信息,解答下列问题:
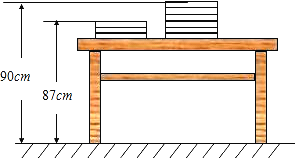
(1)若设每本数学书厚度为![]() ,请列出方程并求出每本书的厚度.
,请列出方程并求出每本书的厚度.
(2)若设桌子的高度为![]() ,请列出方程并求出桌子的高度.
,请列出方程并求出桌子的高度.
(3)请结合(1)(2)的计算,写出数学课本数![]() (本
(本![]() 放在桌子上的最大高度
放在桌子上的最大高度![]() 之间的关系.
之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:

(1)此次共调查了 名学生;
(2)扇形统计图中D所在扇形的圆心角为 ;
(3)将上面的条形统计图补充完整;
(4)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
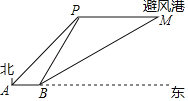
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行_____小时即可到达.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,小莹随机抽查了所住小区n户家庭的月用水量,绘制了下面不完整的统计图.
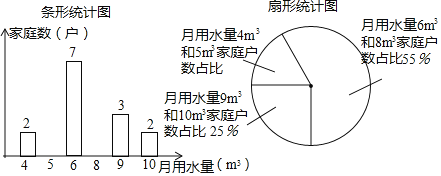
(1)求n并补全条形统计图;
(2)求这n户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;
(3)从月用水量为5m3和和9m3的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入3400元;
营业员B:月销售件数300件,月总收入3700元;
假设营业员的月基本工资为x元,销售每件服装奖动y元.
(1)求x和y的值;
(2)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲服装3件,乙服装2件,丙服袋1件共需390元:如果购买甲服装1件,乙服装2件,丙服装3件共需370元.某顾客想购买甲、乙、丙服装各一件共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 ![]() 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
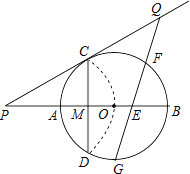
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为 ![]() 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 ![]() 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com