
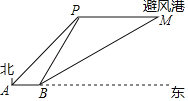
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行_____小时即可到达.(结果保留根号)
【答案】![]()
【解析】
如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,通过解直角△AQP、直角△BPQ求得PQ的长度,即MN的长度,然后通过解直角△BMN求得BM的长度,则易得所需时间.
如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,
在直角△AQP中,∠PAQ=45°,则AQ=PQ=60×1.5+BQ=90+BQ(海里),
所以 BQ=PQ﹣90.
在直角△BPQ中,∠BPQ=30°,则BQ=PQtan30°=![]() PQ(海里),
PQ(海里),
所以 PQ﹣90=![]() PQ,
PQ,
所以 PQ=45(3+![]() )(海里),
)(海里),
所以 MN=PQ=45(3+![]() )(海里),
)(海里),
在直角△BMN中,∠MBN=30°,
所以 BM=2MN=90(3+![]() )(海里),
)(海里),
所以![]() (小时),
(小时),
故答案为:![]() .
.


科目:初中数学 来源: 题型:
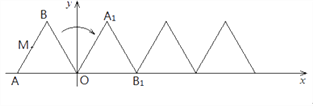
【题目】如图,正△ABO的边长为2,O为坐标原点,A在 ![]() 轴上,B在第二象限.△ABO沿
轴上,B在第二象限.△ABO沿 ![]() 轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是________;翻滚2017次后AB中点M经过的路径长为________.
轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是________;翻滚2017次后AB中点M经过的路径长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线系数”.
(1)任意抛物线都有“抛物线三角形”是______(填“真”或“假”)命题;
(2)若一条抛物线系数为[1,0,-2],则其“抛物线三角形”的面积为________;
(3)若一条抛物线系数为[-1,2b,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;
(4)在(3)的前提下,该抛物线的顶点为A,与x轴交于O,B两点,在抛物线上是否存在一点P,过P作PQ⊥x轴于点Q,使得△BPQ∽△OAB,如果存在,求出P点坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌 A 款汽车,随着汽车的普及,其价格也在不断下降, 今年5月份 A 款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的 A 款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份 A 款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的 B 款汽车,已知 A 款汽车每辆进价为7.5万元,B 款汽车每辆进价为 6 万元,公司预计用不多余105 万元且不少于99 万元的资金购买这两款汽车共15辆,有几种进货方案?
(3)在(2)的前提下,如果 B 款汽车每辆售价为8 万元,为打开 B 款汽车的销路,公司决定每售出一辆 B 款汽车,返还顾客现金 a 万元0 a 2,此时,哪种方案对公司更有利?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月18日至27日(共10天)武汉军运会期间,从19日起武汉体育中心9天中接收观众人数的变化情况如下表(正数表示比前一天多的人数,负数表示经前一天少的人数):
日期 | 19日 | 20日 | 21日 | 2日 | 23日 | 24日 | 25日 | 26日 | 27日 |
人数变化/万人 | +0.5 | +0.7 | +0.8 | -0.4 | -0.6 | +0.2 | +0.3 | +0.5 | +0.2 |
(1)请判断这9天中,游客人数最多和最少的各是哪一天?它们相差多少万人?
(2)如果10月18日观众人数为2万人,平均每人门票100元,请问武汉体育中心在军运会这10天期间门票总收入为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲,乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可贏利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com