
【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
【答案】(1)每台![]() 型挖掘机一小时挖土30立方米,每台
型挖掘机一小时挖土30立方米,每台![]() 型挖据机一小时挖土15立方米;
型挖据机一小时挖土15立方米;
(2)共有三种调配方案.方案一: ![]() 型挖据机7台,
型挖据机7台,![]() 型挖掘机5台;方案二:
型挖掘机5台;方案二: ![]() 型挖掘机8台,
型挖掘机8台,![]() 型挖掘机4台;方案三:
型挖掘机4台;方案三: ![]() 型挖掘机9台,
型挖掘机9台,![]() 型挖掘机3台.当A型挖掘机7台,
型挖掘机3台.当A型挖掘机7台, ![]() 型挖掘机5台的施工费用最低,最低费用为12000元.
型挖掘机5台的施工费用最低,最低费用为12000元.
【解析】(1)根据题意列出方程组即可;
(2)利用总费用不超过12960元求出方案数量,再利用一次函数增减性求出最低费用.
(1)设每台![]() 型,
型,![]() 型挖掘机一小时分别挖土
型挖掘机一小时分别挖土![]() 立方米和
立方米和![]() 立方米,根据题意,得
立方米,根据题意,得
![]()
解得![]()
所以,每台![]() 型挖掘机一小时挖土30立方米,每台
型挖掘机一小时挖土30立方米,每台![]() 型挖据机一小时挖土15立方米.
型挖据机一小时挖土15立方米.
(2)设![]() 型挖掘机有
型挖掘机有![]() 台,总费用为
台,总费用为![]() 元,则
元,则![]() 型挖据机有
型挖据机有![]() 台.根据题意,得
台.根据题意,得
![]()
![]() ,
,
因为![]() ,解得
,解得![]() ,
,
又因为![]() ,解得
,解得![]() ,所以
,所以![]() .
.
所以,共有三种调配方案.
方案一:当![]() 时,
时,![]() ,即
,即![]() 型挖据机7台,
型挖据机7台,![]() 型挖掘机5台;
型挖掘机5台;
方案二:当![]() 时,
时,![]() ,即
,即![]() 型挖掘机8台,
型挖掘机8台,![]() 型挖掘机4台;
型挖掘机4台;
方案三:当![]() 时,
时,![]() ,即
,即![]() 型挖掘机9台,
型挖掘机9台,![]() 型挖掘机3台.
型挖掘机3台.
![]() ,由一次函数的性质可知,
,由一次函数的性质可知,![]() 随
随![]() 的减小而减小,
的减小而减小,
当![]() 时,
时,![]() ,
,
此时![]() 型挖掘机7台,
型挖掘机7台, ![]() 型挖掘机5台的施工费用最低,最低费用为12000元.
型挖掘机5台的施工费用最低,最低费用为12000元.


科目:初中数学 来源: 题型:
【题目】甲,乙两人以相同路线前往距离单位10![]() 的培训中心参加学习.图中
的培训中心参加学习.图中![]() 分别表示甲,乙两人前往目的地所走的路程s
分别表示甲,乙两人前往目的地所走的路程s![]() 随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8
随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8![]() 后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
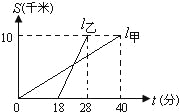
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:

(1)此次共调查了 名学生;
(2)扇形统计图中D所在扇形的圆心角为 ;
(3)将上面的条形统计图补充完整;
(4)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行_____小时即可到达.(结果保留根号)
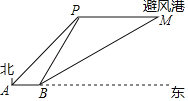
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,小莹随机抽查了所住小区n户家庭的月用水量,绘制了下面不完整的统计图.
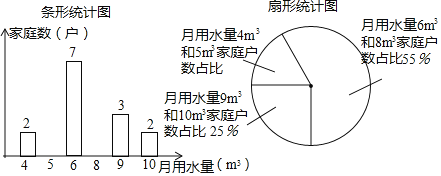
(1)求n并补全条形统计图;
(2)求这n户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;
(3)从月用水量为5m3和和9m3的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入3400元;
营业员B:月销售件数300件,月总收入3700元;
假设营业员的月基本工资为x元,销售每件服装奖动y元.
(1)求x和y的值;
(2)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲服装3件,乙服装2件,丙服袋1件共需390元:如果购买甲服装1件,乙服装2件,丙服装3件共需370元.某顾客想购买甲、乙、丙服装各一件共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ACB中,∠ACB=90°,CE是△ACB的中线,分别过点A、点C作CE和AB的平行线,交于点D.
(1)求证:四边形ADCE是菱形;
(2)若CE=4,且∠DAE=60°,求△ACB的面积.
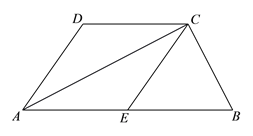
查看答案和解析>>
科目:初中数学 来源: 题型:
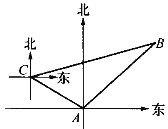
【题目】如图,甲、乙两只捕捞船同时从A港出海捕鱼,甲船以每小时15![]() 千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com