
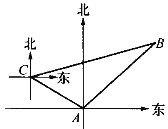
【题目】如图,甲、乙两只捕捞船同时从A港出海捕鱼,甲船以每小时15![]() 千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是多少?
【答案】(1)2;(2)15+15![]() .
.
【解析】
试题分析:(1)根据方向角可以得到∠BCA=45°,∠B=30°,过A作AD⊥BC于点D,在Rt△ACD中,根据三角函数就可求得AD的长,再在直角△ABD中,根据三角函数即可求得AB的长,就可求得时间;(2)求出BC的长,根据(1)中的结果求得时间,即可求得速度.
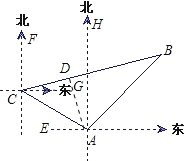
试题解析:(1)如图,过A作AD⊥BC于点D.作CG∥AE交AD于点G.
∵乙船沿东北方向前进,
∴∠HAB=45°,
∵∠EAC=30°,
∴∠CAH=90°-30°=60°
∴∠CAB=60°+45°=105°.
∵CG∥EA,
∴∠GCA=∠EAC=30°.
∵∠FCD=75°,
∴∠BCG=15°,∠BCA=15°+30°=45°,
∴∠B=180°-∠BCA-∠CAB=30°.
在直角△ACD中,∠ACD=45°,AC=2×15![]() =30
=30![]() .
.
AD=ACsin45°=30![]() ×
×![]() =30千米.
=30千米.
CD=ACcos45°=30千米.
在Rt△ABD中,∠B=30°.
则AB=2AD=60千米.
则甲船从C处追赶上乙船的时间是:60÷15-2=2小时;
(2)BC=CD+BD=30+30![]() 千米.
千米.
则甲船追赶乙船的速度是每小时(30+30![]() )÷2=15+15
)÷2=15+15![]() 千米/小时.
千米/小时.
答:甲船从C处追赶上乙船用了2小时,甲船追赶乙船的速度是每小时15+15![]() 千米.
千米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
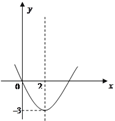
【题目】小明从右边的二次函数y=ax2+bx+c图象中,观察得出了下面的五条信息:①a<0,②c=0,③函数的最小值为-3,④当x<0时,y>0,⑤当0<x1<x2<2时,y1>y2 , (6)对称轴是直线x=2.你认为其中正确的个数为( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲,乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可贏利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.

(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外阅读是提高学生素养的重要途径.某校为了解本校学生课外阅读情况,对九年级学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请根据图中提供的信息,解答下面的问题:
(1)本次抽样调查的样本容量是____ ____;
(2)在条形统计图补中,计算出日人均阅读时间在0.5~1小时的人数是____ ____,并将条形统计图补充完整;
(3)在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角度数____ ____度;
(4)根据本次抽样调查,试估计该市15000名九年级学生中日人均阅读时间在0.5~1.5小时的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列证明:
已知:如图,AB∥CD,直线AE交CD于点C,∠BAC+∠CDF=180°.

求证:AE∥DF.
证明: ∵AB∥CD(____________________________) ,
∴∠BAC=∠DCE(__________________________________________________________________________).
∵∠BAC+∠CDF=180°(已知),
∴____________ +∠CDF=180°(____________________________________).
∴AE∥DF(______________________________________________________________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com