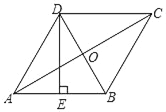
【题目】如图，在菱形ABCD中，AC、BD相交于点O，E为AB的中点，且DE⊥AB，AC＝6，则菱形ABCD的面积是（ ）
A. 18 B. 18
C. 9 D. 6
【答案】D
【解析】
根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，再根据菱形的四条边都相等可得AB=AD，然后求出AB=AD=BD，从而得到△ABD是等边三角形，再根据菱形的对角线互相平分求出AO，再根据直角三角形30度角的性质得OB的长，则得对角线BD的长，根据菱形面积公式：两条对角线乘积一半可得结论．
∵E为AB的中点，DE⊥AB，∴AD=DB．
∵四边形ABCD是菱形，∴AB=AD，∴AD=DB=AB，∴△ABD为等边三角形．
∵四边形ABCD是菱形，∴BD⊥AC于O，AO
AC
6=3．
Rt△AOB中，∵∠OAB=30°，∴OB
，∴BD=2OB=2
，∴菱形ABCD的面积
．
故选D．
科目：初中数学 来源： 题型：
【题目】教材在探索平方差公式时利用了面积法，面积法除了可以帮助我们记忆公式，还可以直观地推导或验证公式，俗称“无字证明”，例如，著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为
，较小的直角边长都为
，斜边长都为
），大正方形的面积可以表示为
，也可以表示为
，由此推导出重要的勾股定理：如果直角三角形两条直角边长为
，斜边长为，则
．
（1）图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导勾股定理．
（2）如图③，在
中，
是
边上的高，
，
，
，设
，求
的值．
（3）试构造一个图形，使它的面积能够解释
，画在如图4的网格中，并标出字母
所表示的线段．
查看答案和解析>>
科目：初中数学 来源： 题型：
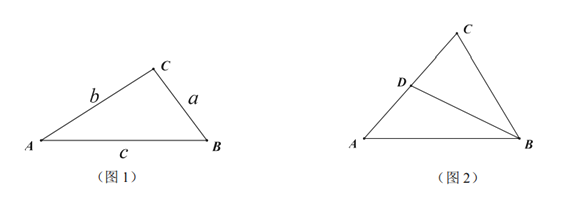
【题目】如图1，
的
所对边分别是
，且
，若满足
，则称为奇异三角形，例如等边三角形就是奇异三角形.
（1）若
，判断是否为奇异三角形，并说明理由；
（2）若
，
，求
的长；
（3）如图2，在奇异三角形中，
，点
是
边上的中点，连结
，将分割成2个三角形，其中
是奇异三角形，
是以
为底的等腰三角形，求
的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列一组图形中点的个数，其中第1个图中共有4个点，第2个图中共有10个点，第3个图中共有19个点，…，按此规律第100个图中共有点的个数是
A. 15151B. 15152C. 15153D. 15154
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列命题是真命题的是( )
A.一组对边平行且有一组对角相等的四边形是平行四边形
B.对角线相等的四边形是矩形
C.一组对边平行且另一组对边相等的四边形是平行四边形
D.对角线互相垂直且相等的四边形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
