解:联立方程组

消去y得,x
2+(a+17)x+38-a=
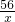
,
即x
3+(a+17)x
2+(38-a)x-56=0,
当x=1时,x
3+(a+17)x
2+(38-a)x-56=0,
∴式子x
3+(a+17)x
2+(38-a)x-56中含有因式(x-1),
分解因式得(x-1)[x
2+(a+18)x+56]=0,(1)
显然x
1=1是方程(1)的一个根,(1,56)是两个函数的图象的一个交点.
因为a是正整数,所以关于x的方程x
2+(a+18)x+56=0,(2)
其判别式△=(a+18)
2-224>0,它一定有两个不同的实数根.
而两个函数的图象的交点都是整点,所以方程(2)的根都是整数,
因此它的判别式△=(a+18)
2-224应该是一个完全平方数.
设(a+18)
2-224=k
2(其中k为非负整数),则(a+18)
2-k
2=224,即(a+18+k)(a+18-k)=224.
显然a+18+k与a+18-k的奇偶性相同,且a+18+k≥18,而224=112×2=56×4=28×8,
所以

或

或

解得

或

或

而a是正整数,所以只可能

或

.
故答案为:a=39或a=12.
分析:先联立两方程,得到关于x的一元二次方程,把此方程分解为两个因式积的形式,再根据一元二次方程根的判别式即可求解.
点评:本题考查的是二次函数与反比例函数的交点问题、根的判别式、整数的奇偶性,涉及面较广,难度较大.

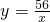 ,如果两个函数的图象的交点都是整点(横坐标和纵坐标都是整数的点),求a的值.
,如果两个函数的图象的交点都是整点(横坐标和纵坐标都是整数的点),求a的值. 消去y得,x2+(a+17)x+38-a=
消去y得,x2+(a+17)x+38-a=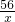 ,
, 或
或 或
或 解得
解得 或
或 或
或
 或
或 .
.

 阅读快车系列答案
阅读快车系列答案