
已知:如图,![]() 是⊙O的直径,点
是⊙O的直径,点![]() 是
是![]() 上任意一点,过点
上任意一点,过点![]() 作弦
作弦![]() 点
点![]() 是
是![]() 上任一点,连结
上任一点,连结![]() 交
交![]() 于
于![]() 连结AC、CF、BD、OD.
连结AC、CF、BD、OD.

1. (1)求证:![]() ;
;
2.(2)猜想:![]() 与
与![]() 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
3. (3)试探究:当点![]() 位于何处时,△
位于何处时,△![]() 的面积与△
的面积与△![]() 的面积之比为1:2?并加以证明.
的面积之比为1:2?并加以证明.
1.(1)证明:∵ 弦CD⊥直径AB于点E, ∴ ![]() .
.
∴ ∠ACD =∠AFC.
又 ∵ ∠CAH=∠FAC,
∴ △ACH∽△AFC(两角对应相等的两个三角形相似).--------------1分
2.(2)猜想:AH·AF=AE·AB.
 证明:连结FB.
证明:连结FB.
∵ AB为直径,∴∠AFB=90°.
又∵ AB⊥CD于点E,∴ ∠AEH=90°.
∴![]() .∵ ∠EAH=∠FAB,
.∵ ∠EAH=∠FAB,
∴ △AHE∽△ABF.
∴ ![]() .
.
∴ AH·AF=AE·AB.------------------------------------------------- -----3分
3.(3)答:当点![]() 位于
位于![]() 的中点(或
的中点(或![]() )时,△
)时,△![]() 的面积与△
的面积与△![]() 的面积之比为1:2 .
的面积之比为1:2 .
证明:设 △![]() 的面积为
的面积为![]() ,△
,△![]() 的面积为
的面积为![]() .
.
∵ 弦CD⊥直径AB于点E, ∴ ![]() =
=![]() ,
,![]() =
=![]() .
.
∵![]() 位于
位于![]() 的中点,∴
的中点,∴![]() .
.
又![]() 是⊙O的直径,∴
是⊙O的直径,∴![]() .
.
∴ .
.
又 由垂径定理知 CE=ED,∴ ![]() .
.
∴ 当点![]() 位于
位于![]() 的中点时,△
的中点时,△![]() 的面积与△
的面积与△![]() 的面
的面
积之比为1:2 . -------------------------------------------------7分
解析:略


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
 22、已知,如图CD是⊙O的切线,C是切点,直径AB的延长线与CD相交于D,连接OC、BC.
22、已知,如图CD是⊙O的切线,C是切点,直径AB的延长线与CD相交于D,连接OC、BC.查看答案和解析>>
科目:初中数学 来源: 题型:
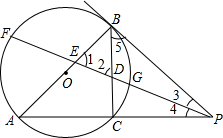 、BC于E、D,交⊙O于F、G,且BE、BD恰好是关于x的方程x2-6x+(m2+4m+13)=0(其中m为实数)的两根.
、BC于E、D,交⊙O于F、G,且BE、BD恰好是关于x的方程x2-6x+(m2+4m+13)=0(其中m为实数)的两根.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2002•西藏)已知,如图AB是⊙O的直径,半径OC⊥AB,弦CD与AB交于点E.
(2002•西藏)已知,如图AB是⊙O的直径,半径OC⊥AB,弦CD与AB交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com