
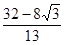 ,
,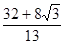
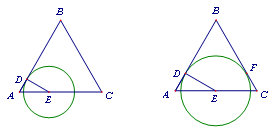
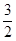 t,在Rt△DME中,DE=AM+EM=3t,在Rt△ADE中,可得AD+DE=AE,即可得到∠ADE=90°,从而证得结论;
t,在Rt△DME中,DE=AM+EM=3t,在Rt△ADE中,可得AD+DE=AE,即可得到∠ADE=90°,从而证得结论;
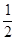 t,DM=
t,DM=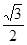 t
t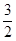 t
t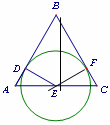
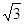 t,
t,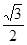 t,
t,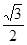 t=4,t=
t=4,t=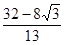
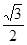 t=4,t=
t=4,t=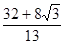 .
.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
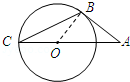
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题



查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
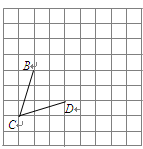
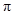 )
)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 cm,阴影部分弓高为6,求弓形的面积;
cm,阴影部分弓高为6,求弓形的面积;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com