
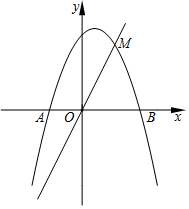 如图,在直角坐标系中,抛物线y=-x2+bx+2与x轴交于A、B两点,与直线y=2x交于点M(1,m).
如图,在直角坐标系中,抛物线y=-x2+bx+2与x轴交于A、B两点,与直线y=2x交于点M(1,m).分析 (1)把点M的坐标先代入直线方程求得m的值;然后把点M的坐标(1,2)代入抛物线方程来求b的值;
(2)由对称的性质得到N(-1,-2),根据点到坐标与图形的性质和平移的性质求得s=2设平移后的直线表达式为y=2x+s,所以设平移后的直线表达式为y=2x+s,与抛物线方程联立方程组,结合根的判别式的符号来求s的取值范围;
(3)在x轴上取一点P(-2,0),以P为圆心,OP为半径作圆,⊙P与抛物线的交点,即是所求作的点G(图中的G与G′).当点G在x轴上方时,利用两边及夹角法推知△GPA∽△BPG.故∠PGA=∠PBG,结合等边对等角得到:∠POG=∠PGO.又由图中角与角间的和差关系推知:∠POG=∠PBG+∠OGB,∠PGO=∠PGA+∠AGO,即∠AGO=∠BGO.同理可证:当点G(G′)在x轴下方时,结论也成立.
解答 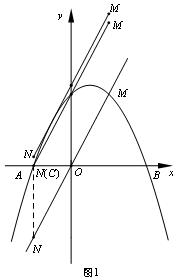 解:(1)把M(1,m)代入y=2x得m=2×1=2.
解:(1)把M(1,m)代入y=2x得m=2×1=2.
把M(1,2)代入y=-x2+bx+2得2=-12+b+2,即b=1.
(2)由(1)得y=-x2+x+2,M(1,2)
因为点N,点M关于原点O对称,所以N(-1,-2)
过点N作CN⊥x轴,交抛物线于C,则C的横坐标为-1.
所以C的纵坐标为-(-1)2+(-1)+2=0.
所以C(-1,0)与A重合.
则CN=AN=2,即当s=2线段MN与抛物线有两个公共点.
设平移后的直线表达式为y=2x+s
由$\left\{\begin{array}{l}y=2x+s\\ y=-{x^2}+x+2\end{array}\right.$得x2+x+s-2=0.
由△=12-4(s-2)=0,得$s=\frac{9}{4}$.
即当$s=\frac{9}{4}$,线段MN与抛物线只有一个公共点.
所以,当线段MN与抛物线有两个公共点时.s取值范围为$2≤s<\frac{9}{4}$.
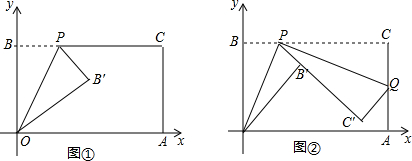
(3)如图,在x轴上取一点P(-2,0),以P为圆心,OP为半径作圆,⊙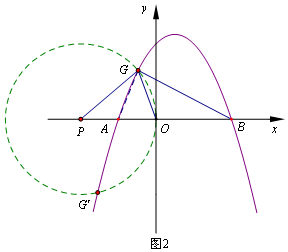 P与抛物线的交点,即是所求作的点G(图中的G与G′).
P与抛物线的交点,即是所求作的点G(图中的G与G′).
理由:
当点G在x轴上方时,由作图可知,
PG=2,PA=1,PB=4.则$\frac{PA}{PG}=\frac{PG}{PB}=\frac{1}{2}$.
又∵∠GPA=∠BPG,
∴△GPA∽△BPG.
∴∠PGA=∠PBG,
∵GP=PB=2,
∴∠POG=∠PGO.
又∠POG=∠PBG+∠OGB,∠PGO=∠PGA+∠AGO,
∴∠AGO=∠BGO.
同理可证:当点G(G′)在x轴下方时,结论也成立.
点评 本题考查了二次函数综合题,解题时涉及到了待定系数法求一次函数、二次函数解析式,函数图象上点的坐标特征,相似三角形的判定与性质,一次函数图象的几何变换以及直线与抛物线的交点问题,综合性比较强,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 “购买某种苹果所花的钱y(元)与购买苹果的重量x(kg)之间的函数关系如图,且每进店购买一次,必须同时购买一个0.4元的塑料袋”,这是某水果店的广告,小娟上午买了苹果1kg,下午又买了2kg,若将她两次花的钱一次性购买此苹果(含塑料袋),则可多买苹果( )
“购买某种苹果所花的钱y(元)与购买苹果的重量x(kg)之间的函数关系如图,且每进店购买一次,必须同时购买一个0.4元的塑料袋”,这是某水果店的广告,小娟上午买了苹果1kg,下午又买了2kg,若将她两次花的钱一次性购买此苹果(含塑料袋),则可多买苹果( )| A. | $\frac{2}{5}$kg | B. | $\frac{2}{3}$kg | C. | $\frac{4}{5}$kg | D. | $\frac{14}{15}$kg |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
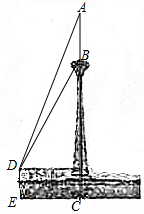 天津广播电视塔是津门十景之一,如图所示,电视塔顶部有一桅杆部分AB,若在距地面高为4.2m的平台D处观测电视塔桅杆顶部A的仰角为67.3°,观测桅杆底部B的仰角为58°.已知点A,B,C在同一条直线上,EC=172m.求桅杆部分AB的高度和天塔AC的高度.(结果保留小数点后一位).参考数据:tan58°≈1.60,tan67.3°≈2.39.
天津广播电视塔是津门十景之一,如图所示,电视塔顶部有一桅杆部分AB,若在距地面高为4.2m的平台D处观测电视塔桅杆顶部A的仰角为67.3°,观测桅杆底部B的仰角为58°.已知点A,B,C在同一条直线上,EC=172m.求桅杆部分AB的高度和天塔AC的高度.(结果保留小数点后一位).参考数据:tan58°≈1.60,tan67.3°≈2.39.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | … |
| 弹簧的长度(cm) | 8 | 8.5 | 9 | 9.5 | 10 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
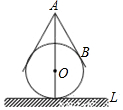 用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为$\frac{720π}{13}$cm2.
用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为$\frac{720π}{13}$cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com