
【题目】为提高饮水质量,越来越多的居民选购家用净水器,一商场抓住商机,从厂家购进了A,B两种型号家用净水器,其数量和进价如表:

为使每台B型号家用净水器的售价是A型号的2倍,且保证售完这批家用净水器的利润不低于1650元,每台A型号家用净水器的售价至少应为多少元?(注:利润=售价-进价)
科目:初中数学 来源: 题型:
【题目】对于实数x,符号[x]表示不大于x的最大整数解,如:[π]=3,[6]=6,[-7.5]=-8.
(1)若[a]=-3,那么a的取值范围是 ______ ;
(2)若![]() =2,求满足条件的所有正整数a.
=2,求满足条件的所有正整数a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
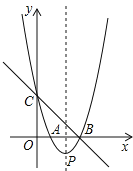
(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com