
【题目】如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有 . (填序号) 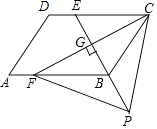
【答案】①②③④
【解析】解:证明:∵BC=EC,
∴∠CEB=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CEB=∠EBF,
∴∠CBE=∠EBF,
∴①BE平分∠CBF,正确;
∵BC=EC,CF⊥BE,
∴∠ECF=∠BCF,
∴②CF平分∠DCB,正确;
∵DC∥AB,
∴∠DCF=∠CFB,
∵∠ECF=∠BCF,
∴∠CFB=∠BCF,
∴BF=BC,
∴③正确;
∵FB=BC,CF⊥BE,
∴B点一定在FC的垂直平分线上,即PB垂直平分FC,
∴PF=PC,故④正确.
所以答案是①②③④.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
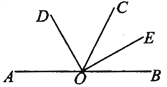
【题目】如图,已知A、O、B三点在一直线上,∠AOC=120°,OD、OE分别是∠AOC,
∠BOC的平分线.
(1)判断OD与OE的位置关系;
(2)当∠AOC大小发生变化时,OD、OE仍分别是∠AOC、∠BOC的平分线,则OD与OE的位置关系是否改变? 请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是 . 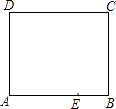
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=﹣2x2+1向右平移1个单位,再向下平移3个单位后所得到的抛物线为( )
A.y=-2(x+1)2-2B.y=-2(x+1)2-4C.y=-2(x-1)2-2D.y=-2(x-1)2-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期,两摞规格相同的数学课本整齐的叠放在讲台上,请根据图中所给出的数据信息,解答下列问题:
(![]() )每本书的高度为__________
)每本书的高度为__________ ![]() ,课桌的高度为__________
,课桌的高度为__________ ![]() .
.
(![]() )当课本数为
)当课本数为![]() (本)时,请写出同样叠放在桌面上的一摞数学课本高出地面的距离__________(用含
(本)时,请写出同样叠放在桌面上的一摞数学课本高出地面的距离__________(用含![]() 的代数式表示).
的代数式表示).
(![]() )桌面上有
)桌面上有![]() 本与题(
本与题(![]() )中相同的数学课本,整齐叠放成一摞,若有
)中相同的数学课本,整齐叠放成一摞,若有![]() 名同学各从中取走
名同学各从中取走![]() 本,求余下的数学课本高出地面的距离(写过程).
本,求余下的数学课本高出地面的距离(写过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22017的值.
解:设S=1+2+22+23+24+…+22017,
将等式两边同时乘以2得,2S=2+22+23+24+25+…+22017+22018,
将下式减去上式得:2S-S=22018-1,即S=22018-1,
所以1+2+22+23+24+…+2201722018-1,
请你依照此法计算:
(1)1+2+22+23+24+…+29;
(2)1+5+52+53+54+…+5n(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:
在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,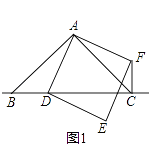
①BC与CF的位置关系为: ,
②BC,DC,CF之间的数量关系为:;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,(1)中的①,②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.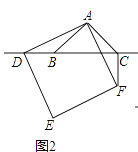
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请直接写出GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
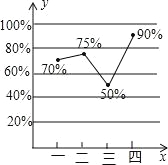
【题目】某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:
(1)若第一季度的汽车销售量为2100辆,求该季的汽车产量;
(2)圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com