
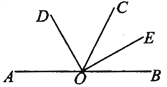
【题目】如图,已知A、O、B三点在一直线上,∠AOC=120°,OD、OE分别是∠AOC,
∠BOC的平分线.
(1)判断OD与OE的位置关系;
(2)当∠AOC大小发生变化时,OD、OE仍分别是∠AOC、∠BOC的平分线,则OD与OE的位置关系是否改变? 请说明理由.
【答案】(1)垂直;(2)不变,理由见解析.
【解析】试题分析:(1)OD⊥OE,由∠AOC=120°,可得∠BOC=60°,再根据角平分线的定义可得∠DOC=60°,∠EOC=30°,从而得∠DOE=90°,即OD⊥OE;
(2)不变, 由角平分线的定义可得∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠COB,从而得∠DOE=90°,从而可得OD与OE的位置关系不发生改变.
∠COB,从而得∠DOE=90°,从而可得OD与OE的位置关系不发生改变.
试题解析:(1)OD⊥OE,理由如下:
∵∠AOC=120°,∴∠BOC=60°,
∵OD是∠AOC的平分线,OE是∠BOC的平分线,
∴∠DOC=60°,∠EOC=30°,
∴∠DOE=60°+30°=90°,
即OD⊥OE;
(2)不变,理由如下:
∵OD,OE分别是∠AOC,∠BOC的平分线,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠COB,
∠COB,
∴∠DOE=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)=![]() ×180°=90°,
×180°=90°,
∴OD⊥OE,
即OD与OE的位置关系不发生改变.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )
A.(a+b)元
B.(3a+2b)元
C.(2a+3b)元
D.5(a+b)元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.

(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上,![]() ,结果精确到0.1)
,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
(1)全等三角形的对应边相等;(2)全等三角形的对应角相等;
(3)全等三角形的周长相等;(4)周长相等的两个三角形相等;
(5)全等三角形的面积相等;(6)面积相等的两个三角形全等.
其中不正确的是( )
A. (4)(5) B. (4)(6) C. (3)(6) D. (3)(4)(5)(6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠DCA的平分线于点F. 
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有 . (填序号) 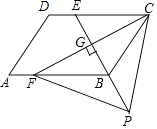
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com