
科目:初中数学 来源: 题型:选择题
 定义:如图,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形构成一个直角三角形,则称点M、N是线段AB的勾股分割点,若AM=2,MN=3,则BN的长为( )
定义:如图,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形构成一个直角三角形,则称点M、N是线段AB的勾股分割点,若AM=2,MN=3,则BN的长为( )| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | $\sqrt{5}$或$\sqrt{13}$ | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,D为等边三角形ABC内的一点,DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为5;②∠ADC=150°;③△ACD'可以由△ABD绕点A逆时针旋转60°得到;④点D到CD'的距离为3;⑤S四边形ABCD′=6+$\frac{25\sqrt{3}}{2}$,其中正确的有( )
如图,D为等边三角形ABC内的一点,DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为5;②∠ADC=150°;③△ACD'可以由△ABD绕点A逆时针旋转60°得到;④点D到CD'的距离为3;⑤S四边形ABCD′=6+$\frac{25\sqrt{3}}{2}$,其中正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=5,AC=3,BC=4,D是BC边上一动点,BE⊥AD,交其延长线于点E,EF⊥AC,交其延长线于点F,则AF的最大值为4.
如图,在△ABC中,AB=5,AC=3,BC=4,D是BC边上一动点,BE⊥AD,交其延长线于点E,EF⊥AC,交其延长线于点F,则AF的最大值为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
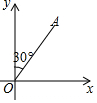 某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.
某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com