
 某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.
某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.分析 依照题意画出图形,根据路程=速度×时间可求出PA、PB,根据PA、PB、AB的长度,利用勾股定理的逆运用即可得出∠APB=90°,结合∠NPA的度数即可求出∠SPB的度数,此题得解.
解答 解:(1)依照题意画出图形,如图所示.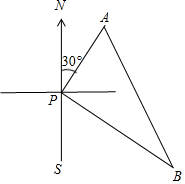
(2)PA=40×15=600(m),PB=40×20=800(m),AB=1000m,
∵6002+8002=10002,
∴PA2+PB2=AB2,
∴△APB为直角三角形,且∠APB=90°.
∵∠NPA=30°,
∴∠SPB=60°,
∴乙客轮的航行方向为南偏东60°
点评 本题考查了勾股定理的应用以及方向角,根据PA、PB、AB的长度,利用勾股定理的逆运用找出∠APB=90°是解题的关键.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
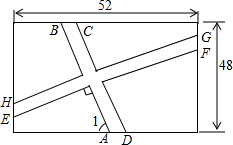 要在一块长52m,宽48m的矩形绿地上修建同样宽的两条互相垂直的甬路.下面是小颖的设计方案,如图所示,BC=HE=2,AB∥CD,HG∥EF,AB⊥EF,∠1=60°,求小颖设计方案中四块绿地的总面积.
要在一块长52m,宽48m的矩形绿地上修建同样宽的两条互相垂直的甬路.下面是小颖的设计方案,如图所示,BC=HE=2,AB∥CD,HG∥EF,AB⊥EF,∠1=60°,求小颖设计方案中四块绿地的总面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
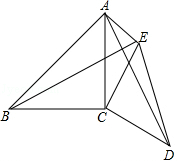 如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE
如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3a>-3b | B. | -$\frac{a}{3}>-\frac{b}{3}$ | C. | 3-a<3-b | D. | a-3<b-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在△ABC中,∠B,∠C的角平分线相交于点O,过O作DE∥BC,交AB于D点,交AC于E点,若BD+EC=6,则DE等于( )
在△ABC中,∠B,∠C的角平分线相交于点O,过O作DE∥BC,交AB于D点,交AC于E点,若BD+EC=6,则DE等于( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com