
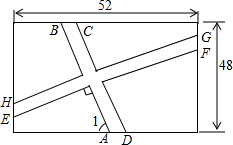
 要在一块长52m,宽48m的矩形绿地上修建同样宽的两条互相垂直的甬路.下面是小颖的设计方案,如图所示,BC=HE=2,AB∥CD,HG∥EF,AB⊥EF,∠1=60°,求小颖设计方案中四块绿地的总面积.
要在一块长52m,宽48m的矩形绿地上修建同样宽的两条互相垂直的甬路.下面是小颖的设计方案,如图所示,BC=HE=2,AB∥CD,HG∥EF,AB⊥EF,∠1=60°,求小颖设计方案中四块绿地的总面积.  学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:解答题
 某地区随机抽取若干名八年级学生进行地理会考模拟测试,并对测试成绩x(分)进行了统计,具体统计结果见表:
某地区随机抽取若干名八年级学生进行地理会考模拟测试,并对测试成绩x(分)进行了统计,具体统计结果见表:| 分数段 | 90<x≤100 | 80<x≤90 | 70<x≤80 | 60<x≤70 | x≤60 |
| 人数 | 1200 | 1461 | 642 | a | 217 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 定义:如图,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形构成一个直角三角形,则称点M、N是线段AB的勾股分割点,若AM=2,MN=3,则BN的长为( )
定义:如图,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形构成一个直角三角形,则称点M、N是线段AB的勾股分割点,若AM=2,MN=3,则BN的长为( )| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | $\sqrt{5}$或$\sqrt{13}$ | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
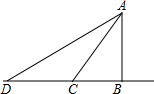 如图,某学校A与直线公路BD的距离AB为3km,与该公路上一车站D相距5km,现要在公路边建一个小商店C,使之与学校A及车站D的距离相等,请你推算一下,该商店应建在距车站D多远处.
如图,某学校A与直线公路BD的距离AB为3km,与该公路上一车站D相距5km,现要在公路边建一个小商店C,使之与学校A及车站D的距离相等,请你推算一下,该商店应建在距车站D多远处.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
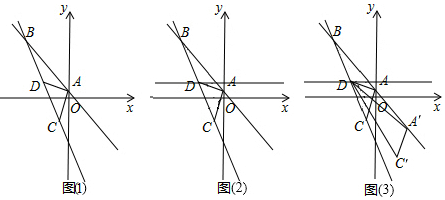
 如图,D为等边三角形ABC内的一点,DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为5;②∠ADC=150°;③△ACD'可以由△ABD绕点A逆时针旋转60°得到;④点D到CD'的距离为3;⑤S四边形ABCD′=6+$\frac{25\sqrt{3}}{2}$,其中正确的有( )
如图,D为等边三角形ABC内的一点,DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为5;②∠ADC=150°;③△ACD'可以由△ABD绕点A逆时针旋转60°得到;④点D到CD'的距离为3;⑤S四边形ABCD′=6+$\frac{25\sqrt{3}}{2}$,其中正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
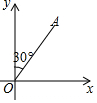 某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.
某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com