解:(1)∵抛物线y=x
2-2mx+m
2-9与y轴交点坐标为(0,-5),
∴-5=m
2-9.
解得:m=±2.
当m=-2,y=0时,x
2+4x-5=0
解得:x
1=-5,x
2=1,
∵抛物线y=x
2-2mx+m
2-9与x轴交于A,B两点(点A在点B的左侧,且OA<OB),
∴m=-2不符合题意,舍去.
∴m=2.
∴抛物线的解析式为y=x
2-4x-5;
(2)过D点作DF⊥x轴于点F,
∴∠DFB=90°
∵MC⊥x轴,
∴∠CMB=90°,
∴∠CMB=∠DFB.
∴CM∥DF.
∵C、D关于抛物线的对称轴对称,
∴CD∥x轴,
∴∠MCD=∠CDF=∠CDP+∠PDF=90°
∵PD⊥BD,
∴∠PDB=∠PDF+∠FDB=90°
∴∠PDC=∠BDF.
∵∠PCD=∠BFD=90°,
∴△PCD∽△BFD.
∴
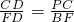
.
当x=1时,y=-8,
∴C(1,-8),D(3,-8),F(3,0),B(5,0),
设P(1,y),
∴
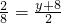
.
解得:
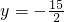
.
∴当P的坐标为
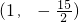
时,PD⊥BD;
(3)假设E点存在,∵MC⊥EM,CD⊥MC,
∴∠EMP=∠PCD=90°.
∴∠MEP+∠MPE=90°
∵PE⊥PD,
∴∠EPD=90°,
∴∠MPE+∠DPC=90°
∴∠MEP=∠CPD.
在△EMP和△PCD中,
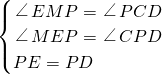
,
∴△EPM≌△PDC(AAS).
∴PM=DC,EM=PC.
设C(x
0,y
0),则D(4-x
0,y
0),
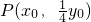
.
∴
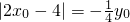
.
∵点C在抛物线y=x
2-4x-5上;
∴y
0═x
02-4x
0-5
∴
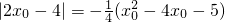
.
当
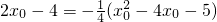
时,
解得:x
01=3,x
02=-7(舍去),
当
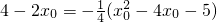
时,
解得:x
03=1,x
04=11(舍去),
∴x
0=1或x
0=3.
∴P(1,-2)或P(3,-2).
∴PC=6.∴ME=PC=6.
∴E(7,0)或E(-3,0).
分析:(1)直接将C点(0,-5)代入y=x
2-2mx+m
2-9根据抛物线与x轴交于A,B两点(点A在点B的左侧,且OA<OB),求出m的值即可;
(2)过D点作DF⊥x轴于点F,根据直角三角形的性质可以得出∠PDC=∠BDF,从而可以求出△PCD∽△BFD,由相似三角形的性质就可以求出结论;
(3)假设E点存在由直角三角形的性质可以得出∠MEP=∠CPD.再根据条件可以得出△EPM≌△PDC就有PM=DC,EM=PC,设C(x
0,y
0),则D(4-x
0,y
0),
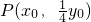
.根据PM=DC就有
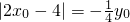
,由C点在抛物线上有
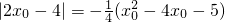
,分两种情况求出x
0的值就可以得出结论.
点评:本题是一道二次函数的综合试题,考查了运用待定系数法求一次函数的解析式的运用,相似三角形的判定及性质的运用,全等三角形的判定及性质的运用,直角三角形的性质的运用,解答时先运用待定系数法求出解析式是关键,解答中灵活运用直角三角形的性质是重点难点.

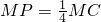 ,作PE⊥PD交x轴于点E,问是否存在这样的点E,使得PE=PD?若存在,求出点E的坐标;若不存在,请说明理由.
,作PE⊥PD交x轴于点E,问是否存在这样的点E,使得PE=PD?若存在,求出点E的坐标;若不存在,请说明理由.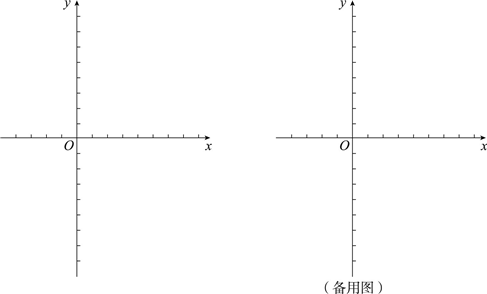

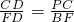 .
.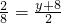 .
.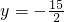 .
.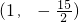 时,PD⊥BD;
时,PD⊥BD;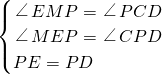 ,
,
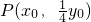 .
.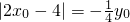 .
. .
. 时,
时, 时,
时, .根据PM=DC就有
.根据PM=DC就有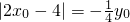 ,由C点在抛物线上有
,由C点在抛物线上有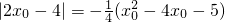 ,分两种情况求出x0的值就可以得出结论.
,分两种情况求出x0的值就可以得出结论.

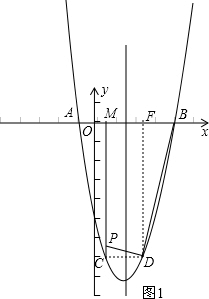
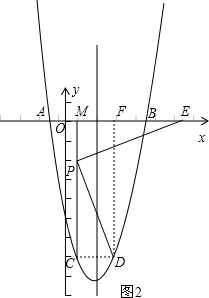
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为