C
分析:先连接AO,延长交BC于D,根据三角形外角性质可知∠BOD=∠1+∠BAO,∠COD=∠CAO+∠3,两式相加易得∠BOC=∠1+∠3+∠BAC,再根据三角形内角和定理可得180°-∠BOC=∠2+∠4,再根据∠1=∠2,∠3=∠4,易证∠1+∠3=180°-∠BOC,再整体代入∠BOC=∠1+∠3+∠BAC,即可求∠BOC.
解答:
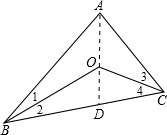
解:连接AO,延长交BC于D,
∵∠BOD=∠1+∠BAO,∠COD=∠CAO+∠3,
∴∠BOD+∠COD=∠1+∠3+∠BAO+∠CAO=∠1+∠3+∠BAC,
即∠BOC=∠1+∠3+∠BAC,
又∵∠3+∠4+∠BOC=180°,
∴180°-∠BOC=∠2+∠4,
∵∠1=∠2,∠3=∠4,
∴∠2+∠4=∠1+∠3,
∴∠1+∠3=180°-∠BOC,
∴∠BOC=180°-∠BOC+∠BAC,
即2∠BOC=180°+∠BAC,
∴∠BOC=130°.
故选C.
点评:本题考查了三角形内角和定理、三角形外角性质.解题的关键是作辅助线,并注意灵活的等量代换.

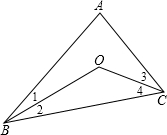 如图,已知:∠1=∠2,∠3=∠4,∠A=80°,则∠BOC等于
如图,已知:∠1=∠2,∠3=∠4,∠A=80°,则∠BOC等于 解:连接AO,延长交BC于D,
解:连接AO,延长交BC于D,

 阅读快车系列答案
阅读快车系列答案 =2,∠ADC=30°
=2,∠ADC=30°