
| A. | ②③④ | B. | ①③④ | C. | ①②④ | D. | ①②③ |
分析 根据抛物线的对称轴公式判断①;求出ax2-4ax=0的判别式△=16a2>0,得出图象与x轴有两个交点,又图象过原点,得到图象与坐标轴只有两个交点,即可判断②;计算方程ax2-4ax-2=0的判别式△的值,即可判断③;根据二次函数的增减性判断④.
解答 解:①二次函数y=ax2-4ax(a>0),
∴对称轴是x=$\frac{4a}{2a}$=2,故①正确;
②∵△=16a2>0,
∴图象与x轴有两个交点,
又∵x=0时y=0,即图象过原点,
∴图象与y轴交点是原点,
∴图象与坐标轴只有两个交点,故②正确;
③∵方程ax2-4ax-2=0的判别式△=16a2+8a,而a>0,
∴△>0,
∴方程ax2-4ax-2=0一定有实数根,故③正确;
④∵二次函数y=ax2-4ax(a>0)开口向上,对称轴是x=2,
∴当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大,
∴当x≤3时,y随x的增大而减小是错误的,故④错误.
故选D.
点评 本题考查了抛物线与x轴的交点,掌握二次函数与一元二次方程的关系、二次函数的性质是解题的关键.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
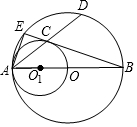 如图,AB是⊙O的直径,AO是⊙O1的直径,⊙O的弦AD交⊙O1于点C,BC的延长线交⊙O于点E.
如图,AB是⊙O的直径,AO是⊙O1的直径,⊙O的弦AD交⊙O1于点C,BC的延长线交⊙O于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 80+0.5x=30 | B. | 0.5x-80=30 | C. | $\frac{80}{x}$-0.5=$\frac{30}{x}$ | D. | $\frac{x}{80}$+0.5=$\frac{x}{30}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC,作CG∥EB,CG与BD、BA分别相交于点F、G,下列说法中:①CF⊥BD;②BC2=BG•BA;③BC2=BF•BD;④CH=CB.正确的个数是 ( )
如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC,作CG∥EB,CG与BD、BA分别相交于点F、G,下列说法中:①CF⊥BD;②BC2=BG•BA;③BC2=BF•BD;④CH=CB.正确的个数是 ( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
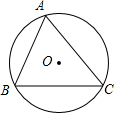 如图,⊙O是△ABC的外接圆,⊙O的半径r=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
如图,⊙O是△ABC的外接圆,⊙O的半径r=2,sinB=$\frac{3}{4}$,则弦AC的长为( )| A. | 4 | B. | 3 | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 采购数量(件) | 2 | 4 | 6 | … |
| A产品单价(元) | 1460 | 1420 | 1380 | … |
| B产品单价(元) | 1280 | 1260 | 1240 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 加图,已知在数轴上点A表示的数是6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴匀速向左运动,设运动时间为t(t>0)秒.
加图,已知在数轴上点A表示的数是6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴匀速向左运动,设运动时间为t(t>0)秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com