
【题目】已知:![]() 为⊙
为⊙![]() 的直径,
的直径,![]() ,弦
,弦![]() ,直线
,直线![]() 与
与![]() 相交于点
相交于点![]() ,弦
,弦![]() 在⊙
在⊙![]() 上运动且保持长度不变,⊙
上运动且保持长度不变,⊙![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() .
.
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,当点![]() 运动至与点
运动至与点![]() 重合时,试判断
重合时,试判断![]() 与
与![]() 是否相等,并说明理由.
是否相等,并说明理由.
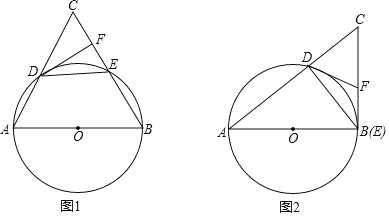
【答案】(1)证明见解析(2)相等
【解析】
试题分析:(1)如图1,连接OD、OE,证得△OAD、△ODE、△OEB、△CDE是等边三角形,进一步证得DF⊥CE即可证得结论;
(2)根据切线的性质以及等腰三角形的性质即可证得结论.
试题解析:(1)如图1,连接OD、OE,
∵AB=2,
∴OA=OD=OE=OB=1,
∵DE=1,
∴OD=OE=DE,
∴△ODE是等边三角形,
∴∠ODE=∠OED=60°,
∵DE∥AB,
∴∠AOD=∠ODE=60°,∠EOB=∠OED=60°,
∴△AOD和△△OE是等边三角形,
∴∠OAD=∠OBE=60°,
∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°,
∴△CDE是等边三角形,
∵DF是⊙O的切线,
∴OD⊥DF,
∴∠EDF=90°﹣60°=30°,
∴∠DFE=90°,
∴DF⊥CE,
∴CF=EF;

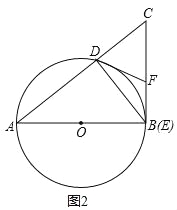
(2)相等;
如图2,点E运动至与点B重合时,BC是⊙O的切线,
∵⊙O的切线DF交BC于点F,
∴BF=DF,
∴∠BDF=∠DBF,
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴∠FDC=∠C,
∴DF=CF,
∴BF=CF.


科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断一个三角形是直角三角形的是( )
A. 三个角的比为1:2:3 B. 三条边满足关系a2=b2﹣c2
C. 三条边的比为1:2:3 D. 三个角满足关系∠B+∠C=∠A
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,△BCF的周长和∠EFC分别等于( )
A.16cm,40°
B.8cm,50°
C.16cm,50°
D.8cm,40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x=﹣1是关于x的一元二次方程ax2+bx﹣2=0(a≠0)的一个根,则2019﹣2a+2b的值等于( )
A.2015B.2017C.2019D.2022
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,2016年石家庄外环线内新栽植树木6120000株,将6120000用科学记数法表示为( )
A.0.612×107
B.6.12×106
C.61.2×105
D.612×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网购成为时下最热的购物方式,同时也带动了快递业的发展.某快递公司更新了包裹分拣设备后,平均每人每天比原先要多分拣50件包裹,现在分拣600件包裹所需的时间与原来分拣450件包裹所需时间相同,现在平均每人每天分拣多少件包裹?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 经过平行四边形
经过平行四边形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() ,抛物线与
,抛物线与![]() 轴的另一交点为
轴的另一交点为![]() .经过点
.经过点![]() 的直线
的直线![]() 将平行四边形
将平行四边形![]() 分割为面积相等的两部分,与抛物线交于另一点
分割为面积相等的两部分,与抛物线交于另一点![]() .点
.点![]() 为直线
为直线![]() 上方抛物线上一动点,设点
上方抛物线上一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的解析式;
(2)当![]() 何值时,
何值时,![]() 的面积最大?并求最大值的立方根;
的面积最大?并求最大值的立方根;
(3)是否存在点![]() 使
使![]() 为直角三角形?若存在,求出
为直角三角形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com